题目内容
6.下列命题:①如果a、b、c为一组勾股数,那么4a、4b、4c仍是勾股数;
②含有30°角的直角三角形的三边长之比是3:4:5;
③如果一个三角形的三边是12、25、21,那么此三角形必是直角三角形;
④一个等腰直角三角形的三边是a、b、c,(a>b=c),那么a2:b2:c2=2:1:1.
其中正确的是( )
| A. | ①② | B. | ①④ | C. | ①③ | D. | ②④ |
分析 ①根据勾股数的定义判断勾股数即可;
②根据直角三角形的性质判断三边的比即可;
③依据勾股定理的逆定理,判定三角形是否为直角三角形;
④根据等腰直角三角形的性质判断三边的平方的比即可.
解答 解:①正确,∵a2+b2=c2,∴(4a)2+(4b)2=(4c)2,
②错误,应为“如果直角三角形的两直角边是3,4,那么斜边必是5”
③错误,∵122+212≠252,∴不是直角三角形;
④正确,∵b=c,c2+b2=2b2=a2,∴a2:b2:c2=2:1:1.
故选B.
点评 此题主要考查勾股定理的逆定理,直角三角形的判定等知识点的综合运用.

练习册系列答案
相关题目
11.下列命题:①三点确定一个圆;②相等的圆心角所对的弦相等;③直径所对的圆周角是直角;④直角三角形的外心是斜边的中点.真命题为( )
| A. | ①②③④ | B. | ②③④ | C. | ③④ | D. | ①③ |
15.如果2xny2与-xym是同类项,那么m、n的值分别为( )
| A. | m=2,n=0 | B. | m=2,n=1 | C. | m=-2,n=-1 | D. | m=-2,n=1 |
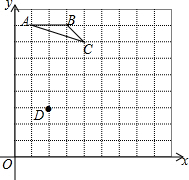 如图,每个小方格都是边长为1个单位的小正方形,A、B、C三点都是格点(每个小方格的顶点叫格点),其中A(1,8),B(3,8),C(4,7).
如图,每个小方格都是边长为1个单位的小正方形,A、B、C三点都是格点(每个小方格的顶点叫格点),其中A(1,8),B(3,8),C(4,7).