题目内容
8.已知α+β=90°,且sinα+cosβ=$\sqrt{3}$,求锐角α.分析 根据一个角的余弦等于它余角的正弦,可得sinα=cosβ,根据特殊角三角函数值,可得答案.
解答 解:由α+β=90°,得sinα=cosβ.
sinα+cosβ=2sinα=$\sqrt{3}$,
sinα=$\frac{\sqrt{3}}{2}$,
α=60°.
点评 本题考查了互为余角的三角函数的关系,利用一个角的余弦等于它余角的正弦得出2sinα的值是解题关键.

练习册系列答案
相关题目
18.已知一元二次方程x2-8x+16=0的两根分别是⊙O1和⊙O2的半径,若O1O2=6,则这两圆的位置关系是( )
| A. | 内含 | B. | 相交 | C. | 外切 | D. | 外离 |
20.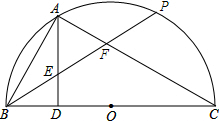 如图所示,已知BC是半圆的直径,P是半圆上一点,过弧BP的中点A作AD⊥BC于点D,BP交AD于点E,交AC于点F,则一定成立的是( )
如图所示,已知BC是半圆的直径,P是半圆上一点,过弧BP的中点A作AD⊥BC于点D,BP交AD于点E,交AC于点F,则一定成立的是( )
 如图所示,已知BC是半圆的直径,P是半圆上一点,过弧BP的中点A作AD⊥BC于点D,BP交AD于点E,交AC于点F,则一定成立的是( )
如图所示,已知BC是半圆的直径,P是半圆上一点,过弧BP的中点A作AD⊥BC于点D,BP交AD于点E,交AC于点F,则一定成立的是( )| A. | AE=EF | B. | AE=AF | C. | AF=EF | D. | AE=EF=AF |
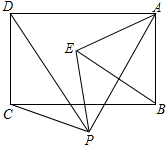 如图,P是矩形ABCD下方一点,将△PCD绕P点顺时针旋转60°后恰好D点与A点重合,得到△PEA,连接EB.
如图,P是矩形ABCD下方一点,将△PCD绕P点顺时针旋转60°后恰好D点与A点重合,得到△PEA,连接EB.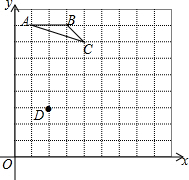 如图,每个小方格都是边长为1个单位的小正方形,A、B、C三点都是格点(每个小方格的顶点叫格点),其中A(1,8),B(3,8),C(4,7).
如图,每个小方格都是边长为1个单位的小正方形,A、B、C三点都是格点(每个小方格的顶点叫格点),其中A(1,8),B(3,8),C(4,7).