Question

11．已知反比例函数y=$\frac{1-2m}{x}$（m为常数）的图象在第一、三象限．
（1）求m的取值范围；
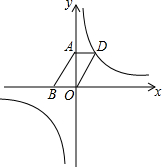
（2）如图，若该反比例函数的图象经过平行四边形ABOD的顶点D，点A、B的坐标分别为（0，3），（-2，0）．求出函数解析式．

Answer 1

分析 （1）根据反比例函数的性质得1-2m＞0，然后解不等式得到m的取值范围；
（2）①根据平行四边形的性质得AD∥OB，AD=OB=2，易得D点坐标为（2，3），然后根据反比例函数图象上点的坐标特征得1-2m=6，则反比例函数解析式为y=$\frac{6}{x}$．

解答 解：（1）根据题意得1-2m＞0，
解得m＜$\frac{1}{2}$；
（2）∵四边形ABOC为平行四边形，
∴AD∥OB，AD=OB=2，而A点坐标为（0，3），
∴D点坐标为（2，3），
∴1-2m=2×3=6，
∴反比例函数解析y=$\frac{6}{x}$．

点评 本题考查了待定系数法求反比例函数的解析式、反比例函数图象上点的坐标特征、平行四边形的性质；根据平行四边形的性质求得D的坐标是解题的关键．