题目内容
1. 如图,在扇形AOB中,∠AOB=90°,$\widehat{AC}$=$\widehat{BC}$,点D在OB上,点E在OB的延长线上,当正方形CDEF的边长为2$\sqrt{2}$时,则阴影部分的面积为2π-4.
如图,在扇形AOB中,∠AOB=90°,$\widehat{AC}$=$\widehat{BC}$,点D在OB上,点E在OB的延长线上,当正方形CDEF的边长为2$\sqrt{2}$时,则阴影部分的面积为2π-4.
分析 连结OC,根据勾股定理可求OC的长,根据题意可得出阴影部分的面积=扇形BOC的面积-三角形ODC的面积,依此列式计算即可求解.
解答 解:∵在扇形AOB中∠AOB=90°,且 $\widehat{AC}$=$\widehat{BC}$,
$\widehat{AC}$=$\widehat{BC}$,
∴∠COD=45°,
∴OC=$\sqrt{(2\sqrt{2})^{2}+(2\sqrt{2})^{2}}$=4,
∴阴影部分的面积=扇形BOC的面积-三角形ODC的面积
=$\frac{45π×{4}^{2}}{360}$-$\frac{1}{2}$×(2$\sqrt{2}$)2
=2π-4.
故答案为2π-4.
点评 考查了正方形的性质和扇形面积的计算,解题的关键是得到扇形半径的长度.

练习册系列答案
 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
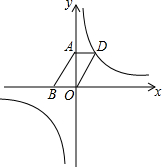 已知反比例函数y=$\frac{1-2m}{x}$(m为常数)的图象在第一、三象限.
已知反比例函数y=$\frac{1-2m}{x}$(m为常数)的图象在第一、三象限.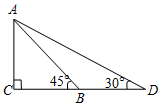 如图,为安全起见,幼儿园打算加长滑梯AB,将其倾斜角由45°降至30°,已知滑梯AB的长为4m,点D,B,C在同一水平地面上,那么加长后的滑梯AD的长是
如图,为安全起见,幼儿园打算加长滑梯AB,将其倾斜角由45°降至30°,已知滑梯AB的长为4m,点D,B,C在同一水平地面上,那么加长后的滑梯AD的长是
 如图,在四边形ABCD中,点E在对角线AC上,AB∥DE,∠ACB=∠EDA,AB=EA,求证:AC=ED.
如图,在四边形ABCD中,点E在对角线AC上,AB∥DE,∠ACB=∠EDA,AB=EA,求证:AC=ED. 如图,△ABC中,AB=AC,∠B=∠C=40°,点E、F在BC边上,∠AEF=70°,∠AFE=60°,求线段BE、EF、CF围成的三角形的各内角度数.
如图,△ABC中,AB=AC,∠B=∠C=40°,点E、F在BC边上,∠AEF=70°,∠AFE=60°,求线段BE、EF、CF围成的三角形的各内角度数.