题目内容
6.如图,一架梯子的长度为15米,斜靠在墙上,梯子低部离墙底端为9米.(1)这个梯子顶端离地面有12米;
(2)如果梯子的底部沿水平方向向外滑动了4米,那么梯子的顶端下滑了几米?(结果用二次根式表示)
分析 (1)直接根据勾股定理求出AC的长即可;
(2)先根据梯子的顶端下滑了4米求出A′C的长,再根据勾股定理求出B′C的长,进而可得出结论.
解答  解:(1)梯子顶端离地面的距离AC=$\sqrt{1{5}^{2}-{9}^{2}}$=12(米),
解:(1)梯子顶端离地面的距离AC=$\sqrt{1{5}^{2}-{9}^{2}}$=12(米),
故答案为:12米;
(2)底部离墙的距离B′C=9+4=13米,由勾股定理得此时梯子的顶端离地面的距离A′C=$\sqrt{1{5}^{2}-(9+4)^{2}}$=2$\sqrt{14}$ 米,
∴梯子的顶端下滑了AA′=(12-2$\sqrt{14}$ )米.
点评 此题主要考查了勾股定理的应用,关键是掌握勾股定理:在任何一个直角三角形中,两条直角边长的平方之和一定等于斜边长的平方.

练习册系列答案
 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案
相关题目
15.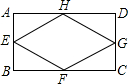 如图所示,在矩形ABCD中,E,F,G,H分别为边AB,BC,CD,DA的中点,若AB=2cm,AD=4cm,则四边形EFGH的面积为( )
如图所示,在矩形ABCD中,E,F,G,H分别为边AB,BC,CD,DA的中点,若AB=2cm,AD=4cm,则四边形EFGH的面积为( )
 如图所示,在矩形ABCD中,E,F,G,H分别为边AB,BC,CD,DA的中点,若AB=2cm,AD=4cm,则四边形EFGH的面积为( )
如图所示,在矩形ABCD中,E,F,G,H分别为边AB,BC,CD,DA的中点,若AB=2cm,AD=4cm,则四边形EFGH的面积为( )| A. | 2cm2 | B. | 4cm2 | C. | 6cm2 | D. | 8cm2 |
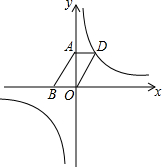 已知反比例函数y=$\frac{1-2m}{x}$(m为常数)的图象在第一、三象限.
已知反比例函数y=$\frac{1-2m}{x}$(m为常数)的图象在第一、三象限.