题目内容
11.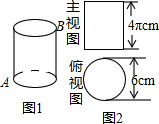 图中圆柱的主视图与俯视图如图所示,一只蚂蚁从A点沿着圆柱的侧面爬行到B点的最短路线长为( )
图中圆柱的主视图与俯视图如图所示,一只蚂蚁从A点沿着圆柱的侧面爬行到B点的最短路线长为( )| A. | (6+4π)cm | B. | 2$\sqrt{9+{π}^{2}}$cm | C. | 7πcm | D. | 5πcm |
分析 首先根据圆锥的主视图和俯视图的尺寸确定展开矩形的长和宽,利用勾股定理求得对角线的长即可.
解答 解:把圆柱侧面展开,展开图如图所示,点A,B的最短距离为线段AB的长,
∵BC=4πcm,AC为底面半圆弧长,即AC=$\frac{1}{2}$×6•π=3π(cm),
∴AB=$\sqrt{(3π)^{2}+(4π)^{2}}$=5π(cm),
故选:D
点评 本题主要考查几何体的展开图与最短路径问题,要求两点间的最短线段,就要把这两点放到一个平面内,即把圆柱的侧面展开再计算.

练习册系列答案
相关题目
20.△ABC为等腰直角三角形,∠ACB=90°,AC=BC=2,P为线段AB上一动点,D为BC上中点,则PC+PD的最小值为( )
| A. | $\sqrt{3}$ | B. | 3 | C. | $\sqrt{5}$ | D. | $\sqrt{2}+1$ |
2. 如图,△ABC和△DBE中,AB=CB,DB=EB,∠ABC=∠DBE=50°.若∠BDC=25°,AD=4,DE=$\sqrt{13}$,则CD的长为( )
如图,△ABC和△DBE中,AB=CB,DB=EB,∠ABC=∠DBE=50°.若∠BDC=25°,AD=4,DE=$\sqrt{13}$,则CD的长为( )
 如图,△ABC和△DBE中,AB=CB,DB=EB,∠ABC=∠DBE=50°.若∠BDC=25°,AD=4,DE=$\sqrt{13}$,则CD的长为( )
如图,△ABC和△DBE中,AB=CB,DB=EB,∠ABC=∠DBE=50°.若∠BDC=25°,AD=4,DE=$\sqrt{13}$,则CD的长为( )| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | $\frac{\sqrt{13}}{2}$ | D. | 2 |
3.下列是张悦、王强和赵涵的对话,张悦:“从学校向西直走500米,再向北直走100米就到医院了”.王强:“从学校向南直走300米,再向西直走200米就到电影院了.”赵涵:“火车站在电影院正北方向的200米处.”,则医院与火车站相距( )
| A. | 100$\sqrt{3}$米 | B. | 200米 | C. | 300米 | D. | 500米 |
20.下列式之中,属于最简二次根式的是( )
| A. | $\sqrt{\frac{1}{3}}$ | B. | $\sqrt{20}$ | C. | $\sqrt{30}$ | D. | $\sqrt{1.5}$ |