题目内容
20.△ABC为等腰直角三角形,∠ACB=90°,AC=BC=2,P为线段AB上一动点,D为BC上中点,则PC+PD的最小值为( )| A. | $\sqrt{3}$ | B. | 3 | C. | $\sqrt{5}$ | D. | $\sqrt{2}+1$ |
分析 作D关于AB的对称点F,连接CF交AB于P,连接PD,BF,则AB垂直平分DF,于是可得PF=PD,BD=BF,即可求得∠CBF=90°,根据勾股定理即可得到结论.
解答  解:作D关于AB的对称点F,连接CF交AB于P,则CF的长度=PC+PD的最小值,连接PD,BF,
解:作D关于AB的对称点F,连接CF交AB于P,则CF的长度=PC+PD的最小值,连接PD,BF,
则AB垂直平分DF,
∴PF=PD,BD=BF=$\frac{1}{2}$BC=1,∠FBP=∠DBP,
∵△ABC为等腰直角三角形,AC=BC,
∴∠ACB=45°,
∴∠CBF=90°,
∴CF2=BC2+BF2=5,
∴CF=$\sqrt{5}$,
∴PC+PD的最小值是$\sqrt{5}$.
故选C.
点评 此题考查了线路最短的问题,确定动点P何位置时,使PC+PD的值最小是关键.

练习册系列答案
相关题目
11.矩形具有而平行四边形不一定具有的性质是( )
| A. | 对角线互相平分 | B. | 两组对角相等 | C. | 对角线相等 | D. | 两组对边相等 |
8.下列各组数中,以它们为边长的线段不能构成直角三角形的是( )
| A. | 1,$\sqrt{2}$,$\sqrt{3}$ | B. | 3,4,5 | C. | 5,12,13 | D. | 2,2,3 |
5.已知∠A的两边与∠B的两边互相平行,且∠A=20°,则∠B的度数为( )
| A. | 20° | B. | 80° | C. | 160° | D. | 20°或160° |
12.下列图形中既是中心对称图形又是轴对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
11.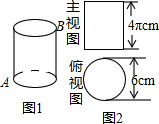 图中圆柱的主视图与俯视图如图所示,一只蚂蚁从A点沿着圆柱的侧面爬行到B点的最短路线长为( )
图中圆柱的主视图与俯视图如图所示,一只蚂蚁从A点沿着圆柱的侧面爬行到B点的最短路线长为( )
 图中圆柱的主视图与俯视图如图所示,一只蚂蚁从A点沿着圆柱的侧面爬行到B点的最短路线长为( )
图中圆柱的主视图与俯视图如图所示,一只蚂蚁从A点沿着圆柱的侧面爬行到B点的最短路线长为( )| A. | (6+4π)cm | B. | 2$\sqrt{9+{π}^{2}}$cm | C. | 7πcm | D. | 5πcm |
 据调查,超速行驶是引发交通事故的主要原因之一,所以规定以下情境中的速度不得超过15m/s,在一条笔直公路BD的上方A处有一探测仪,如平面几何图,AD=24m,∠D=90°,第一次探测到一辆轿车从B点匀速向D点行驶,测得∠ABD=31°,2秒后到达C点,测得∠ACD=50°(tan31°≈0.6,tan50°≈1.2,结果精确到1m)
据调查,超速行驶是引发交通事故的主要原因之一,所以规定以下情境中的速度不得超过15m/s,在一条笔直公路BD的上方A处有一探测仪,如平面几何图,AD=24m,∠D=90°,第一次探测到一辆轿车从B点匀速向D点行驶,测得∠ABD=31°,2秒后到达C点,测得∠ACD=50°(tan31°≈0.6,tan50°≈1.2,结果精确到1m)