题目内容
1．解不等式组$\left\{\begin{array}{l}{2x+5≤3（x+2）}\\{2x-\frac{1+3x}{2}＜1}\end{array}\right.$，并将其解集在数轴上表示出来．分析 分别求出每一个不等式的解集，根据口诀：“大小小大中间找”确定不等式组的解集，再根据“大于向右，小于向左，包括端点用实心，不包括端点用空心”的原则在数轴上将解集表示出来．
解答 解：解不等式2x+5≤3（x+2），得：x≥-1，
解不等式2x-$\frac{1+3x}{2}$＜1，得：x＜3，
∴不等式组的解集为：-1≤x＜3，
其解集在数轴上表示为：
点评 本题考查的是解一元一次不等式组，正确求出每一个不等式解集是基础，熟知“同大取大；同小取小；大小小大中间找；大大小小找不到”的原则是解答此题的关键．
练习册系列答案
相关题目
11．
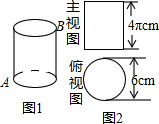图中圆柱的主视图与俯视图如图所示，一只蚂蚁从A点沿着圆柱的侧面爬行到B点的最短路线长为（ ）
图中圆柱的主视图与俯视图如图所示，一只蚂蚁从A点沿着圆柱的侧面爬行到B点的最短路线长为（ ）| A． | （6+4π）cm | B． | 2$\sqrt{9+{π}^{2}}$cm | C． | 7πcm | D． | 5πcm |
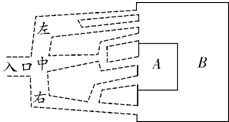如图是“密室逃脱俱乐部”的通路俯视图，一同学进入入口后，可任选一条通道过关．
在如图所示的正方形网格中，每个小正方形的边长为1，格点三角形（顶点在网格线的交点的三角形）△ABC的顶点A、C的坐标分别为（-4，5）、（-1，3）．