题目内容
 如图,在平面直角坐标中,直角梯形OABC的边OC、OA分别在x轴、y轴上,AB∥OC,∠AOC=90°,∠BCO=45°,BC=12
如图,在平面直角坐标中,直角梯形OABC的边OC、OA分别在x轴、y轴上,AB∥OC,∠AOC=90°,∠BCO=45°,BC=12| 2 |
(1)求点B的坐标;
(2)若直线DE交梯形对角线BO于点D,交y轴于点E,且OE=4,∠OFE=45°,求直线DE的解析式;
(3)求点D的坐标.
考点:一次函数综合题
专题:综合题
分析:(1)过B作BG⊥x轴,交x轴于点G,由题意得到三角形BCG为等腰直角三角形,根据BC的长求出CG与BG的长,根据OC-CG求出OG的长,确定出B坐标即可;
(2)由题意得到三角形EOF为等腰直角三角形,确定出E与F的坐标,设直线DE解析式为y=kx+b,把E与F代入求出k与b的值,确定出直线DE解析式;
(3)设直线OB解析式为y=mx,把B坐标代入求出m的值,确定出OB解析式,与直线DE解析式联立求出D坐标即可.
(2)由题意得到三角形EOF为等腰直角三角形,确定出E与F的坐标,设直线DE解析式为y=kx+b,把E与F代入求出k与b的值,确定出直线DE解析式;
(3)设直线OB解析式为y=mx,把B坐标代入求出m的值,确定出OB解析式,与直线DE解析式联立求出D坐标即可.
解答: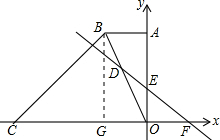 解:(1)过B作BG⊥x轴,交x轴于点G,
解:(1)过B作BG⊥x轴,交x轴于点G,
在Rt△BCG中,∠BCO=45°,BC=12
,
∴BG=CG=12,
∵C(-18,0),即OC=18,
∴OG=OC-CG=18-12=6,
则B=(-6,12);
(2)∵∠EOF=90°,∠OFE=45°,
∴△OEF为等腰直角三角形,
∴OE=OF=4,即E(0,4),F(4,0),
设直线DE解析式为y=kx+b,
把E与F坐标代入得:
,
解得:k=-1,b=4,
∴直线DE解析式为y=-x+4;
(3)设直线OB解析式为y=mx,把B(-6,12)代入得:m=-2,
∴直线OB解析式为y=-2x,
联立得:
,
解得:
,
则D(-4,8).
 解:(1)过B作BG⊥x轴,交x轴于点G,
解:(1)过B作BG⊥x轴,交x轴于点G,在Rt△BCG中,∠BCO=45°,BC=12
| 2 |
∴BG=CG=12,
∵C(-18,0),即OC=18,
∴OG=OC-CG=18-12=6,
则B=(-6,12);
(2)∵∠EOF=90°,∠OFE=45°,
∴△OEF为等腰直角三角形,
∴OE=OF=4,即E(0,4),F(4,0),
设直线DE解析式为y=kx+b,
把E与F坐标代入得:
|
解得:k=-1,b=4,
∴直线DE解析式为y=-x+4;
(3)设直线OB解析式为y=mx,把B(-6,12)代入得:m=-2,
∴直线OB解析式为y=-2x,
联立得:
|
解得:
|
则D(-4,8).
点评:此题属于一次函数综合题,涉及的知识有:坐标与图形性质,待定系数法求一次函数解析式,以及等腰直角三角形的判定与性质,熟练掌握待定系数法是解本题的关键.

练习册系列答案
相关题目
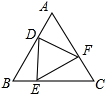 如图,等边△ABC中,DE⊥BC,DF⊥AB,EF⊥AC,说明△DEF为等边三角形.
如图,等边△ABC中,DE⊥BC,DF⊥AB,EF⊥AC,说明△DEF为等边三角形.

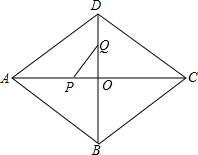 如图,在菱形ABCD中,AC、BD交于点O,AD=15,AO=12.动点P以每秒2个单位的速度从点A出发,沿AC向点C匀速运动.同时,动点Q以每秒1个单位的速度从点D出发,沿DB向点B匀速运动.当其中有一点到达终点时,另一点也停止运动.设运动的时间为t秒.
如图,在菱形ABCD中,AC、BD交于点O,AD=15,AO=12.动点P以每秒2个单位的速度从点A出发,沿AC向点C匀速运动.同时,动点Q以每秒1个单位的速度从点D出发,沿DB向点B匀速运动.当其中有一点到达终点时,另一点也停止运动.设运动的时间为t秒.