题目内容
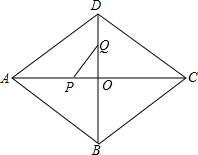 如图,在菱形ABCD中,AC、BD交于点O,AD=15,AO=12.动点P以每秒2个单位的速度从点A出发,沿AC向点C匀速运动.同时,动点Q以每秒1个单位的速度从点D出发,沿DB向点B匀速运动.当其中有一点到达终点时,另一点也停止运动.设运动的时间为t秒.
如图,在菱形ABCD中,AC、BD交于点O,AD=15,AO=12.动点P以每秒2个单位的速度从点A出发,沿AC向点C匀速运动.同时,动点Q以每秒1个单位的速度从点D出发,沿DB向点B匀速运动.当其中有一点到达终点时,另一点也停止运动.设运动的时间为t秒.(1)求线段DO的长.
(2)设运动过程中△POQ两直角边的和为y,请求出y与t的函数关系式.
(3)请直接写出,在整个运动过程中,使△POQ与△AOD相似时所有t的值.
考点:相似形综合题
专题:
分析:(1)根据菱形的对角线互相垂直平分的性质得到直角△AOD,在该直角三角形中利用勾股定理来求线段DO的长度;
(2)需要分类讨论:点P在线段OA上、点Q在线段OD上;点P在线段OC上,点Q在线段OD上;点P在线段OC上,点Q在线段OB上;
(3)需要分类讨论:△POQ∽△AOD、△QOP∽△AOD,利用相似三角形的对应边成比例求得相应线段的长度,从而求得相应的时间.
(2)需要分类讨论:点P在线段OA上、点Q在线段OD上;点P在线段OC上,点Q在线段OD上;点P在线段OC上,点Q在线段OB上;
(3)需要分类讨论:△POQ∽△AOD、△QOP∽△AOD,利用相似三角形的对应边成比例求得相应线段的长度,从而求得相应的时间.
解答:解:(1)∵四边形ABCD是菱形,
∴AC⊥BD.
在Rt△AOD中,AD=15,AO=12
由勾股定理得:
OD=
=
=9.
(2)①当0≤t≤6时,OP=12-2t,OQ=9-t,则OP+OQ=12-2t+9-t=-3t+21
即:y=-3t+21;
②当6<t≤9时,OP=2t-12,OQ=9-t,则OP+OQ=2t-12+9-t=t-3
即:y=t-3;
③当9<t≤12时,OP=2t-12,OQ=t-9,则OP+OQ=2t-12+t-9=3t-21
即:y=3t-21;
综上所述:y=
;
(3)①当0≤t≤6时,△POQ∽△AOD,则
=
,即
=
,解得 t=0,此时△POQ与△AOD重合;
②当0≤t≤6时,△QOP∽△AOD,则
=
,即
=
,解得 t=
;
③当6<t≤9时,△POQ∽△AOD,则
=
,即
=
,解得 t=
;
④当6<t≤9时,△QOP∽△AOD,则
=
,即
=
,解得 t=
;
⑤当9<t≤12时,△POQ∽△AOD,则
=
,即
=
,解得 t=0,不合题意,舍去;
⑥当9<t≤12时,△QOP∽△AOD,则
=
,即
=
,解得 t=
,不合题意,舍去;
综上所述,t=0或
或
或
.
∴AC⊥BD.
在Rt△AOD中,AD=15,AO=12
由勾股定理得:
OD=
| AD2-AO2 |
| 152-122 |
(2)①当0≤t≤6时,OP=12-2t,OQ=9-t,则OP+OQ=12-2t+9-t=-3t+21
即:y=-3t+21;
②当6<t≤9时,OP=2t-12,OQ=9-t,则OP+OQ=2t-12+9-t=t-3
即:y=t-3;
③当9<t≤12时,OP=2t-12,OQ=t-9,则OP+OQ=2t-12+t-9=3t-21
即:y=3t-21;
综上所述:y=
|

(3)①当0≤t≤6时,△POQ∽△AOD,则
| OP |
| OA |
| OQ |
| OD |
| 12-2t |
| 12 |
| 9-t |
| 9 |
②当0≤t≤6时,△QOP∽△AOD,则
| OP |
| OD |
| OQ |
| OA |
| 2t-12 |
| 9 |
| 9-t |
| 12 |
| 21 |
| 5 |
③当6<t≤9时,△POQ∽△AOD,则
| OP |
| OA |
| OQ |
| OD |
| 2t-12 |
| 12 |
| 9-t |
| 9 |
| 36 |
| 5 |
④当6<t≤9时,△QOP∽△AOD,则
| OP |
| OD |
| OQ |
| OA |
| 2t-12 |
| 9 |
| 9-t |
| 12 |
| 75 |
| 11 |
⑤当9<t≤12时,△POQ∽△AOD,则
| OP |
| OA |
| OQ |
| OD |
| 2t-12 |
| 12 |
| t-9 |
| 9 |
⑥当9<t≤12时,△QOP∽△AOD,则
| OP |
| OD |
| OQ |
| OA |
| 2t-12 |
| 9 |
| t-9 |
| 12 |
| 21 |
| 5 |
综上所述,t=0或
| 21 |
| 5 |
| 36 |
| 5 |
| 75 |
| 11 |
点评:本题综合考查了相似三角形的判定与性质,菱形的性质,勾股定理以及函数关系式的书写.解答(2)、(3)题时,一定要结合图形,分类讨论来解答,以防漏解或错解.

练习册系列答案
 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案
相关题目
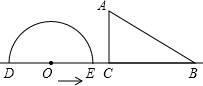 如图,形如量角器的半圆O的直径DE=12cm,形如三角板的△ABC中,∠ACB=90°,∠ABC=30°,BC=12cm半圆O以2cm/s的速度从左向右运动,在运动过程中,点D、E始终在直线BC上.设运动时间为t(s),当t=0s时,半圆O在△ABC的左侧,OC=8cm.
如图,形如量角器的半圆O的直径DE=12cm,形如三角板的△ABC中,∠ACB=90°,∠ABC=30°,BC=12cm半圆O以2cm/s的速度从左向右运动,在运动过程中,点D、E始终在直线BC上.设运动时间为t(s),当t=0s时,半圆O在△ABC的左侧,OC=8cm. 如图,在平面直角坐标中,直角梯形OABC的边OC、OA分别在x轴、y轴上,AB∥OC,∠AOC=90°,∠BCO=45°,BC=12
如图,在平面直角坐标中,直角梯形OABC的边OC、OA分别在x轴、y轴上,AB∥OC,∠AOC=90°,∠BCO=45°,BC=12 在Rt△ABC中,CD是斜边AB上的高,已知BC=
在Rt△ABC中,CD是斜边AB上的高,已知BC=