题目内容
阅读下列材料,然后解答问题.
经过正四边形(即正方形)各顶点的圆叫做这个正四边形的外接圆,圆心是正四边形的对称中心,这个正四边形叫做这个圆的内接正四边形.
如图,正方形ABCD内接于⊙O,⊙O的面积为S1,正方形ABCD的面积为S2.以圆心O为顶点作∠MON,使∠MON=90°.将∠MON绕点O旋转,OM、ON分别与⊙O交于点E、F,分别与正方形ABCD的边交于点G、H.设由OE、OF、
及正方形ABCD的边围成的图形(阴影部分)的面积为S.
(1)当OM经过点A时(如图①),则S、S1、S2之间的关系为: (用含S1、S2的代数式表示);
(2)当OM⊥AB于G时(如图②),则(1)中的结论仍然成立吗?请说明理由;
(3)当∠MON旋转到任意位置时(如图③),则(1)中的结论仍然成立吗?请说明理由.

经过正四边形(即正方形)各顶点的圆叫做这个正四边形的外接圆,圆心是正四边形的对称中心,这个正四边形叫做这个圆的内接正四边形.
如图,正方形ABCD内接于⊙O,⊙O的面积为S1,正方形ABCD的面积为S2.以圆心O为顶点作∠MON,使∠MON=90°.将∠MON绕点O旋转,OM、ON分别与⊙O交于点E、F,分别与正方形ABCD的边交于点G、H.设由OE、OF、
 |
| EF |
(1)当OM经过点A时(如图①),则S、S1、S2之间的关系为:
(2)当OM⊥AB于G时(如图②),则(1)中的结论仍然成立吗?请说明理由;
(3)当∠MON旋转到任意位置时(如图③),则(1)中的结论仍然成立吗?请说明理由.

考点:圆的综合题
专题:
分析:(1)结合正方形的性质及等腰直角三角形的性质,容易得出结论;
(2)仍然成立,可证得四边形OGHB为正方形,则可求出阴影部分的面积为扇形OEF的面积减去正方形OGBH的面积;
(3)仍然成立,过O作OR⊥AB,OS⊥BC,垂足分别为R、S,则可证明△ORG≌△OSH,可得出四边形ORBS的面积=四边形OGBH的面积,再利用扇形OEF的面积减正方形ORBS的面积即可得出结论.
(2)仍然成立,可证得四边形OGHB为正方形,则可求出阴影部分的面积为扇形OEF的面积减去正方形OGBH的面积;
(3)仍然成立,过O作OR⊥AB,OS⊥BC,垂足分别为R、S,则可证明△ORG≌△OSH,可得出四边形ORBS的面积=四边形OGBH的面积,再利用扇形OEF的面积减正方形ORBS的面积即可得出结论.
解答:解:(1)当OM经过点A时由正方形的性质可知:∠MON=90°,
∴S△OAB=
S正方形ABCD=
S2,S扇形OEF=
S圆O=
S1,
∴S=S扇形OEF-S△OAB=
S圆O-
S正方形ABCD=
S1-
S2=
(S1-S2),
故答案为:S=
(S1-S2);
(2)结论仍然成立,理由如下:
∵∠EOF=90°,
∴S扇形OEF=
S圆O=
S1
∵∠OGB=∠EOF=∠ABC=90°,
∴四边形OGBH为矩形,
∵OM⊥AB,
∴BG=
AB=
BC=BH,
∴四边形OGBH为正方形,
∴S四边形OGBH=BG2=(
AB)2=
S2,
∴S=S扇形OEF-S四边形OGBH=
S1-
S2=
(S1-S2);
(3)(1)中的结论仍然成立,理由如下:
∵∠EOF=90°,
∴S扇形OEF=
S圆O=
,
 过O作OR⊥AB,OS⊥BC,垂足分别为R、S,
过O作OR⊥AB,OS⊥BC,垂足分别为R、S,
由(2)可知四边形ORBS为正方形,
∴OR=OS,
∵∠ROS=90°,∠MON=90°,
∴∠ROG=∠SOH=90°-∠GOS,
在△ROG和△SOH中,
,
∴△ROG≌△SOH(ASA),
∴S△ORG=S△OSH,
∴S四边形OGBH=S正方形ORBS,
由(2)可知S正方形ORBS=
S2,
∴S四边形OGBH=
S2,
∴S=S扇形OEF-S四边形OGBH=
(S1-S2).
∴S△OAB=
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
∴S=S扇形OEF-S△OAB=
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
故答案为:S=
| 1 |
| 4 |
(2)结论仍然成立,理由如下:
∵∠EOF=90°,
∴S扇形OEF=
| 1 |
| 4 |
| 1 |
| 4 |
∵∠OGB=∠EOF=∠ABC=90°,
∴四边形OGBH为矩形,
∵OM⊥AB,
∴BG=
| 1 |
| 2 |
| 1 |
| 2 |
∴四边形OGBH为正方形,
∴S四边形OGBH=BG2=(
| 1 |
| 2 |
| 1 |
| 4 |
∴S=S扇形OEF-S四边形OGBH=
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
(3)(1)中的结论仍然成立,理由如下:
∵∠EOF=90°,
∴S扇形OEF=
| 1 |
| 4 |
| 1 |
| 4 |
 过O作OR⊥AB,OS⊥BC,垂足分别为R、S,
过O作OR⊥AB,OS⊥BC,垂足分别为R、S,由(2)可知四边形ORBS为正方形,
∴OR=OS,
∵∠ROS=90°,∠MON=90°,
∴∠ROG=∠SOH=90°-∠GOS,
在△ROG和△SOH中,
|
∴△ROG≌△SOH(ASA),
∴S△ORG=S△OSH,
∴S四边形OGBH=S正方形ORBS,
由(2)可知S正方形ORBS=
| 1 |
| 4 |
∴S四边形OGBH=
| 1 |
| 4 |
∴S=S扇形OEF-S四边形OGBH=
| 1 |
| 4 |
点评:本题主要考查圆的有关计算及正方形的性质、三角形全等的判定和性质等知识的综合运用,求阴影部分的面积主要有两种方法,即“割”或“补”把阴影部分的面积分成其他图形面积的和或差来求解,这是本题解题的关键.

练习册系列答案
相关题目
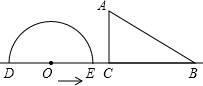 如图,形如量角器的半圆O的直径DE=12cm,形如三角板的△ABC中,∠ACB=90°,∠ABC=30°,BC=12cm半圆O以2cm/s的速度从左向右运动,在运动过程中,点D、E始终在直线BC上.设运动时间为t(s),当t=0s时,半圆O在△ABC的左侧,OC=8cm.
如图,形如量角器的半圆O的直径DE=12cm,形如三角板的△ABC中,∠ACB=90°,∠ABC=30°,BC=12cm半圆O以2cm/s的速度从左向右运动,在运动过程中,点D、E始终在直线BC上.设运动时间为t(s),当t=0s时,半圆O在△ABC的左侧,OC=8cm. 如图,方格纸中每个小方格的边长为1,作一个三边都是无理数,且面积最大的钝角三角形,求出三边的长.
如图,方格纸中每个小方格的边长为1,作一个三边都是无理数,且面积最大的钝角三角形,求出三边的长. 如图,在平面直角坐标中,直角梯形OABC的边OC、OA分别在x轴、y轴上,AB∥OC,∠AOC=90°,∠BCO=45°,BC=12
如图,在平面直角坐标中,直角梯形OABC的边OC、OA分别在x轴、y轴上,AB∥OC,∠AOC=90°,∠BCO=45°,BC=12