题目内容
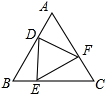如图，等边△ABC中，DE⊥BC，DF⊥AB，EF⊥AC，说明△DEF为等边三角形．考点：等边三角形的判定与性质
专题：证明题
分析：利用等边三角形的性质和直角三角形的性质可得出∠BDE=30°，从而可得出∠EDF=60°，同理可得∠DEF=60°，从而可得出结论．
解答：证明：∵DE⊥BC，
∴∠DEB=90°，
又∵△ABC为等边三角形，
∴∠ABC=60°
∴∠BDE=90-60=30°，
又∵FD⊥AB，
∴∠BDF=90°，
∴∠EDF=∠BDF-∠BDE=90°-30°=60°，
同理：∠DEF=60°，
∴△DEF为等边三角形．
∴∠DEB=90°，
又∵△ABC为等边三角形，
∴∠ABC=60°
∴∠BDE=90-60=30°，
又∵FD⊥AB，
∴∠BDF=90°，
∴∠EDF=∠BDF-∠BDE=90°-30°=60°，
同理：∠DEF=60°，
∴△DEF为等边三角形．
点评：本题主要考查等边三角形的性质和判定，利用条件得到∠EDF=60°是解题的关键．
练习册系列答案
相关题目
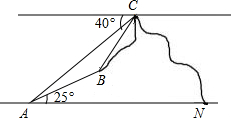如图，MN表示水平地面，由地面上A处测得山上B处的仰角是25°，由山顶C处测得B处的俯角是40°．若AB：BC=2：3，求由A处测得C处的仰角（结果精确到0.1°）．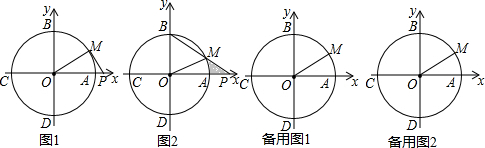
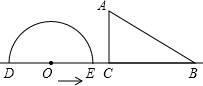如图，形如量角器的半圆O的直径DE=12cm，形如三角板的△ABC中，∠ACB=90°，∠ABC=30°，BC=12cm半圆O以2cm/s的速度从左向右运动，在运动过程中，点D、E始终在直线BC上．设运动时间为t（s），当t=0s时，半圆O在△ABC的左侧，OC=8cm．
如图，在平面直角坐标中，直角梯形OABC的边OC、OA分别在x轴、y轴上，AB∥OC，∠AOC=90°，∠BCO=45°，BC=12