题目内容
20.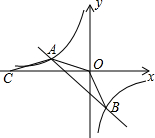 如图,直线AB与反比例函数的图象交于A(-4,m)、B(2,n)两点,点C在x轴上,AO=AC,△OAC的面积为8.
如图,直线AB与反比例函数的图象交于A(-4,m)、B(2,n)两点,点C在x轴上,AO=AC,△OAC的面积为8.(1)求反比例函数的解析式.
(2)求cos∠OBA的值.
分析 (1)因为△ACO是等腰三角形,根据三角形面积公式即可求出m,得点A坐标,用待定系数法可以求出反比例函数的解析式.
(2)欲求cos∠OBA,因为cos∠OBA=$\frac{BE}{OB}$,只要求出OB、BE即可,利用两点间距离公式可求出OB、BE.
解答  解:(1)设反比例函数为y=$\frac{k}{x}$,
解:(1)设反比例函数为y=$\frac{k}{x}$,
∵△OAC的面积为8,AO=AC,A(-4,m)
∴点C(-8,0),$\frac{1}{2}$•8•m=8,
∴m=2,
∴点A(-4,2),
∵反比例函数的图象经过A(-4,2)、B(2,n)两点,
∴k=-8,n=-4,
∴点B坐标(2,-4),
∴反比例函数解析式为y=-$\frac{8}{x}$.
(2)如图作OE⊥AB于E,由(1)可知,OA=OB=2$\sqrt{5}$,AB=6$\sqrt{2}$,
∵OA=OB,OE⊥AB,
∴AE=EB=3$\sqrt{2}$,
∴cos∠OBA=$\frac{EB}{BO}$=$\frac{3\sqrt{2}}{2\sqrt{5}}$=$\frac{3\sqrt{10}}{10}$.
点评 本题考查反比例函数与一次函数的交点问题、三角函数等知识,学会待定系数法求函数解析式,记住三角函数的定义,构造直角三角形是解决问题的关键,属于中考常考题型.

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案
相关题目
5.计算:$\sqrt{3}×\sqrt{6}$的结果是( )
| A. | $9\sqrt{2}$ | B. | $3\sqrt{2}$ | C. | $2\sqrt{3}$ | D. | $3\sqrt{6}$ |
12.计算:
(1)2(a+1)2+(a+2)(1-2a)
(2)$(\frac{{{x^2}+4}}{{2{x^2}-4x}}-\frac{2}{x-2})÷\frac{{{x^2}-4}}{2x}$.
(1)2(a+1)2+(a+2)(1-2a)
(2)$(\frac{{{x^2}+4}}{{2{x^2}-4x}}-\frac{2}{x-2})÷\frac{{{x^2}-4}}{2x}$.
10.某校为实施国家“营养早餐”工程,食堂用甲、乙两种原料配制成某种营养食品,已知这两种原料的维生素C含量及购买这两种原料的价格如下表:
现要配制这种营养食品20千克,要求每千克至少含有9600单位的维生素C.设购买甲种原料x千克.
(1)至少需要购买甲种原料多少千克?
(2)设食堂用于购买这两种原料的总费用为y元,求y与x的函数关系式.并说明购买甲种原料多少千克时,总费用最少?最少费用是多少?
| 原料 维生素C及价格 | 甲种原料 | 乙种原料 |
| 维生素C(单位/千克) | 600 | 400 |
| 原料价格(元/千克) | 9 | 5 |
(1)至少需要购买甲种原料多少千克?
(2)设食堂用于购买这两种原料的总费用为y元,求y与x的函数关系式.并说明购买甲种原料多少千克时,总费用最少?最少费用是多少?
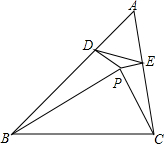 如图,在△ABC中内取一点,使∠PBA=∠PCA,作PD⊥AB于点D,PE⊥AC于点E,求证:DE的垂直平分线必过BC的中点M.
如图,在△ABC中内取一点,使∠PBA=∠PCA,作PD⊥AB于点D,PE⊥AC于点E,求证:DE的垂直平分线必过BC的中点M.