题目内容
14.在平面直角坐标系中,(1)已知点P(a-1,3a+6)在y轴上,求点P的坐标;
(2)已知两点A(-3,m),B(n,4),若AB∥x轴,点B在第一象限,求m的值,并确定n的取值范围;
(3)在(1)(2)的条件下,如果线段AB的长度是5,求以P、A、B为顶点的三角形的面积S.
分析 (1)根据y轴上点的横坐标为0列方程求出a的值,再求解即可;
(2)根据第一象限内点的横坐标是正数,平行于x轴的直线上的点的纵坐标相等解答;
(3)先确定出点P到AB的距离,再根据三角形的面积公式列式计算即可得解.
解答 解:(1)∵点P(a-1,3a+6)在y轴上,
∴a-1=0,
解得a=1,
所以,3a+6=3×1+6=9,
故P(0,9);
(2)∵AB∥x轴,
∴m=4,
∵点B在第一象限,
∴n>0,
∴m=4,n>0;
(3)∵AB=5,A、B的纵坐标都为4,
∴点P到AB的距离为9-4=5,
∴以P、A、B为顶点的三角形的面积S=$\frac{1}{2}$×5×5=12.5.
点评 本题考查了点的坐标,两点间的距离,三角形的面积,熟练掌握坐标轴上点的坐标特征是解题的关键.

练习册系列答案
 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目
3. 把一张对边互相平行的纸条折成如图所示的样子,EF是折痕,如果∠EFB=32°,那么下列结论:①∠CEF=32°;②∠AEF=148°;③∠BGE=64°;④∠BFD=116°正确的有( )
把一张对边互相平行的纸条折成如图所示的样子,EF是折痕,如果∠EFB=32°,那么下列结论:①∠CEF=32°;②∠AEF=148°;③∠BGE=64°;④∠BFD=116°正确的有( )
 把一张对边互相平行的纸条折成如图所示的样子,EF是折痕,如果∠EFB=32°,那么下列结论:①∠CEF=32°;②∠AEF=148°;③∠BGE=64°;④∠BFD=116°正确的有( )
把一张对边互相平行的纸条折成如图所示的样子,EF是折痕,如果∠EFB=32°,那么下列结论:①∠CEF=32°;②∠AEF=148°;③∠BGE=64°;④∠BFD=116°正确的有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
9. 已知一次函数y=kx+b的图象如图所示,则该函数的表达式可能是( )
已知一次函数y=kx+b的图象如图所示,则该函数的表达式可能是( )
 已知一次函数y=kx+b的图象如图所示,则该函数的表达式可能是( )
已知一次函数y=kx+b的图象如图所示,则该函数的表达式可能是( )| A. | y=2x+2 | B. | y=2x-2 | C. | y=-3x+3 | D. | y=-x-4 |
19.小夏是一位善于观察、勤于动脑的学生.一天,他从2017年某个月日历表中随机框取了相邻的四个数(如图所示),分别用a,b,c,d表示.略加思考后,他写出了三个关系式:①a+c=b+d;②c-a=b-d;③ac-bd=7.其中正确的有( )
| 2017年 月 农历丙申(猴)年辛丑月 建国68年 | ||||||
| 日 | 一 | 二 | 三 | 四 | 五 | 六 |
| 1 初五 | 2 初六 | 3 立夏初七 | 4 初八 | |||
| a | d | |||||
| b | c | |||||
| A. | 3个 | B. | 2个 | C. | 1个 | D. | 0个 |
4. 如图,在平面直角坐标系中,边长为1的正方形OA1B1C1的两边在坐标轴上,以它的对角线OB1,为边作正方形OB1B2C2,再以OB1B2C2正方形的对角线OB2为边作正方形OB2B2C3,依此类推…,则正方形OB99B100C100的顶点B100的坐标是( )
如图,在平面直角坐标系中,边长为1的正方形OA1B1C1的两边在坐标轴上,以它的对角线OB1,为边作正方形OB1B2C2,再以OB1B2C2正方形的对角线OB2为边作正方形OB2B2C3,依此类推…,则正方形OB99B100C100的顶点B100的坐标是( )
 如图,在平面直角坐标系中,边长为1的正方形OA1B1C1的两边在坐标轴上,以它的对角线OB1,为边作正方形OB1B2C2,再以OB1B2C2正方形的对角线OB2为边作正方形OB2B2C3,依此类推…,则正方形OB99B100C100的顶点B100的坐标是( )
如图,在平面直角坐标系中,边长为1的正方形OA1B1C1的两边在坐标轴上,以它的对角线OB1,为边作正方形OB1B2C2,再以OB1B2C2正方形的对角线OB2为边作正方形OB2B2C3,依此类推…,则正方形OB99B100C100的顶点B100的坐标是( )| A. | (2100,0) | B. | (0,250) | C. | (-250,0) | D. | (0,-2100) |
 如图,AB是电线杆,从距离地面12m高的A处,向离电杆5m的B处埋线,并埋入地下1.5m深,求拉线长多少米?
如图,AB是电线杆,从距离地面12m高的A处,向离电杆5m的B处埋线,并埋入地下1.5m深,求拉线长多少米? 如图,A,B在一水池的两侧,若BE=DE,∠B=∠D=90°,点A,E,C在同一条直线上,CD=8cm,则水池宽AB=8m.
如图,A,B在一水池的两侧,若BE=DE,∠B=∠D=90°,点A,E,C在同一条直线上,CD=8cm,则水池宽AB=8m.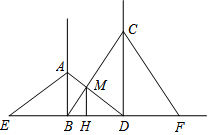 如图,工地上两根电灯杆相距a米,分别在高为4米、6米的A、C处用铁丝将两杆固定,则铁丝AD与铁丝BC的交点M处离地面米的高MH=$\frac{12}{5}$m.
如图,工地上两根电灯杆相距a米,分别在高为4米、6米的A、C处用铁丝将两杆固定,则铁丝AD与铁丝BC的交点M处离地面米的高MH=$\frac{12}{5}$m.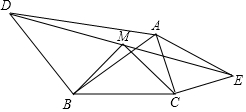 己知:如图,若△ABD和△ACE为等腰Rt△,AB=DB,AC=CE,M为DE中点,求证:△BMC为等腰Rt△.
己知:如图,若△ABD和△ACE为等腰Rt△,AB=DB,AC=CE,M为DE中点,求证:△BMC为等腰Rt△.