题目内容
6.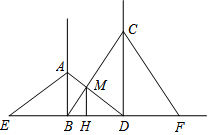 如图,工地上两根电灯杆相距a米,分别在高为4米、6米的A、C处用铁丝将两杆固定,则铁丝AD与铁丝BC的交点M处离地面米的高MH=$\frac{12}{5}$m.
如图,工地上两根电灯杆相距a米,分别在高为4米、6米的A、C处用铁丝将两杆固定,则铁丝AD与铁丝BC的交点M处离地面米的高MH=$\frac{12}{5}$m.
分析 先证明△DMH∽△DAB得到$\frac{MH}{AB}$=$\frac{DH}{DB}$,再证明△BMH∽△BCD得到$\frac{MH}{CD}$=$\frac{BH}{BD}$,利用比例性质得到$\frac{MH}{AB}$+$\frac{MH}{CD}$=1,则$\frac{1}{MH}$=$\frac{1}{AB}$+$\frac{1}{CD}$,然后把AB=4,CD=6代入计算即可.
解答 解:∵MH∥AB,
∴△DMH∽△DAB,
∴$\frac{MH}{AB}$=$\frac{DH}{DB}$①,
∵MH∥CD,
∴△BMH∽△BCD,
∴$\frac{MH}{CD}$=$\frac{BH}{BD}$②,
①+②得$\frac{MH}{AB}$+$\frac{MH}{CD}$=$\frac{DH+BH}{BD}$=1,
∴$\frac{1}{MH}$=$\frac{1}{AB}$+$\frac{1}{CD}$=$\frac{1}{4}$+$\frac{1}{6}$=$\frac{5}{12}$,
∴MH=$\frac{12}{5}$,
即M处离地面米的高MH为$\frac{12}{5}$m.
故答案为$\frac{12}{5}$m.
点评 本题考查了相似三角形的应用:常常构造“A”型或“X”型相似图,然后利用相似比计算相应线段的长.

练习册系列答案
 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案
相关题目
17.两根木条,一根长30cm,一根长16cm,将它们一端重合且放在同一直线上,此时,两根木条的中点之间的距离为( )
| A. | 7cm | B. | 23cm | C. | 7cm或23cm | D. | 14cm或46cm |
1.一辆小汽车在告诉公路上从静止到起动10秒内的速度经测量如下表:
(1)上表反映了哪两个变量之间的关系?哪个是自变量?哪个是因变量?
(2)如果用时间t表示时间,v表示速度,那么随着t的变化,v的变化趋势是什么?
(3)当t每增加1秒,v的变化情况相同吗?在哪个时间段内,v增加的最快?
(4)若高速公路上小汽车行驶速度的上限为120千米/小时,试估计大约还需几秒这辆小汽车的速度就将达到这个上限.
| 时间(秒) | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 速度(米/秒) | 0 | 0.3 | 1.3 | 2.8 | 1.9 | 7.6 | 11.0 | 14.1 | 18.4 | 24.2 | 28.9 |
(2)如果用时间t表示时间,v表示速度,那么随着t的变化,v的变化趋势是什么?
(3)当t每增加1秒,v的变化情况相同吗?在哪个时间段内,v增加的最快?
(4)若高速公路上小汽车行驶速度的上限为120千米/小时,试估计大约还需几秒这辆小汽车的速度就将达到这个上限.
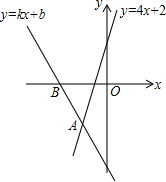 如图,直线y=kx+b经过点B(-2,0)与直线y=4x+2相交于点A,与y轴交于C(0,-4),则不等式4x+2<kx+b的解集为x<-1.
如图,直线y=kx+b经过点B(-2,0)与直线y=4x+2相交于点A,与y轴交于C(0,-4),则不等式4x+2<kx+b的解集为x<-1. 如图,在△ABC中,AD是∠BAC的平分线,E,F分别为AB,AC上的点,若DE=DF,且AE>AF,求证:∠EDF与∠BAF互补(提示:作DM⊥AB于点M,DN⊥AC于点N)
如图,在△ABC中,AD是∠BAC的平分线,E,F分别为AB,AC上的点,若DE=DF,且AE>AF,求证:∠EDF与∠BAF互补(提示:作DM⊥AB于点M,DN⊥AC于点N)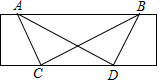 已知:如图,直尺的宽度为2cm,A、B两点在直尺的一条边上,AB=8cm,C、D两点在直尺的另一条边上.若∠ACB=∠ADB=90°,则C、D两点之间的距离为4$\sqrt{3}$cm.
已知:如图,直尺的宽度为2cm,A、B两点在直尺的一条边上,AB=8cm,C、D两点在直尺的另一条边上.若∠ACB=∠ADB=90°,则C、D两点之间的距离为4$\sqrt{3}$cm.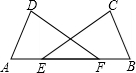 如图,E、F为线段AB上的两点,AF=BE,C、D为线段AB同侧的两点,∠C=∠D,∠A=∠B.
如图,E、F为线段AB上的两点,AF=BE,C、D为线段AB同侧的两点,∠C=∠D,∠A=∠B.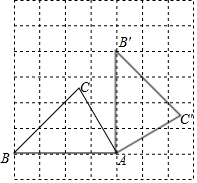 如图,△ABC的顶点A,B都在格点上,将△ABC绕点A顺时针旋转得到相应的△AB′C′,且点B的对应点B′也在格点上,则∠CAC′的度数为90°.
如图,△ABC的顶点A,B都在格点上,将△ABC绕点A顺时针旋转得到相应的△AB′C′,且点B的对应点B′也在格点上,则∠CAC′的度数为90°.