题目内容
9. 已知一次函数y=kx+b的图象如图所示,则该函数的表达式可能是( )
已知一次函数y=kx+b的图象如图所示,则该函数的表达式可能是( )| A. | y=2x+2 | B. | y=2x-2 | C. | y=-3x+3 | D. | y=-x-4 |
分析 根据图象在坐标平面内的位置关系确定k,b的取值范围,从而求解.
解答 解:∵由图可知一次函数y=kx+b的图象经过第一、三、四象限,
∴k、b的符号为k>0,b<0,
符合条件的有B,
故选B.
点评 本题主要考查一次函数图象在坐标平面内的位置与k、b的关系.解答本题注意理解:直线y=kx+b所在的位置与k、b的符号有直接的关系.k>0时,直线必经过一、三象限;k<0时,直线必经过二、四象限;b>0时,直线与y轴正半轴相交;b=0时,直线过原点;b<0时,直线与y轴负半轴相交.

练习册系列答案
 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案
相关题目
17.两根木条,一根长30cm,一根长16cm,将它们一端重合且放在同一直线上,此时,两根木条的中点之间的距离为( )
| A. | 7cm | B. | 23cm | C. | 7cm或23cm | D. | 14cm或46cm |
1.一辆小汽车在告诉公路上从静止到起动10秒内的速度经测量如下表:
(1)上表反映了哪两个变量之间的关系?哪个是自变量?哪个是因变量?
(2)如果用时间t表示时间,v表示速度,那么随着t的变化,v的变化趋势是什么?
(3)当t每增加1秒,v的变化情况相同吗?在哪个时间段内,v增加的最快?
(4)若高速公路上小汽车行驶速度的上限为120千米/小时,试估计大约还需几秒这辆小汽车的速度就将达到这个上限.
| 时间(秒) | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 速度(米/秒) | 0 | 0.3 | 1.3 | 2.8 | 1.9 | 7.6 | 11.0 | 14.1 | 18.4 | 24.2 | 28.9 |
(2)如果用时间t表示时间,v表示速度,那么随着t的变化,v的变化趋势是什么?
(3)当t每增加1秒,v的变化情况相同吗?在哪个时间段内,v增加的最快?
(4)若高速公路上小汽车行驶速度的上限为120千米/小时,试估计大约还需几秒这辆小汽车的速度就将达到这个上限.

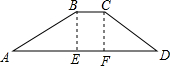 如图,水库大坝的横截面是梯形,坝顶宽5米,坝高20米,斜坡AB的坡比为1:2.5,斜坡CD的坡比为1:2,求大坝的截面面积.
如图,水库大坝的横截面是梯形,坝顶宽5米,坝高20米,斜坡AB的坡比为1:2.5,斜坡CD的坡比为1:2,求大坝的截面面积.
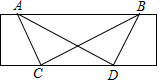 已知:如图,直尺的宽度为2cm,A、B两点在直尺的一条边上,AB=8cm,C、D两点在直尺的另一条边上.若∠ACB=∠ADB=90°,则C、D两点之间的距离为4$\sqrt{3}$cm.
已知:如图,直尺的宽度为2cm,A、B两点在直尺的一条边上,AB=8cm,C、D两点在直尺的另一条边上.若∠ACB=∠ADB=90°,则C、D两点之间的距离为4$\sqrt{3}$cm.