题目内容
2. 如图,A,B在一水池的两侧,若BE=DE,∠B=∠D=90°,点A,E,C在同一条直线上,CD=8cm,则水池宽AB=8m.
如图,A,B在一水池的两侧,若BE=DE,∠B=∠D=90°,点A,E,C在同一条直线上,CD=8cm,则水池宽AB=8m.
分析 由于BE=DE,∠B=∠D,对顶角相等,利用“角边角”,可以判断两个三角形全等,从而AB=CD=8m.
解答 解:在△ABE和△CDE中$\left\{\begin{array}{l}{∠ABE=∠CDE}\\{BE=DE}\\{∠AEB=∠DEC}\end{array}\right.$,
∴△ABE≌△CDE(ASA),
∴CD=AB=8m.
故答案为:8.
点评 此题主要考查了全等三角形的应用,根据题意熟练应用全等三角形的判定方法是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
17.两根木条,一根长30cm,一根长16cm,将它们一端重合且放在同一直线上,此时,两根木条的中点之间的距离为( )
| A. | 7cm | B. | 23cm | C. | 7cm或23cm | D. | 14cm或46cm |
7. 如图是自动测风仪记录的风力随时间变化的图象,它反映了某市春季一天连续12个小时风力变化情况,则下列说法正确的是( )
如图是自动测风仪记录的风力随时间变化的图象,它反映了某市春季一天连续12个小时风力变化情况,则下列说法正确的是( )
 如图是自动测风仪记录的风力随时间变化的图象,它反映了某市春季一天连续12个小时风力变化情况,则下列说法正确的是( )
如图是自动测风仪记录的风力随时间变化的图象,它反映了某市春季一天连续12个小时风力变化情况,则下列说法正确的是( )| A. | 在8时至14时,风力不断增大 | B. | 在8时至12时,风力最大为7级 | ||
| C. | 8时风力最小 | D. | 20时风力最小 |
12.如图,下列条件中,能判定DE∥AC的是( )
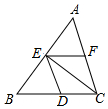

| A. | ∠FEC=∠BCE | B. | ∠FEC=∠FCE | C. | ∠EDC+∠ACB=180° | D. | ∠DEF+∠EDC=180° |
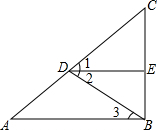 在下列括号中填写推理理由:如图,∠1=∠2,DE⊥BC,AB⊥BC,
在下列括号中填写推理理由:如图,∠1=∠2,DE⊥BC,AB⊥BC,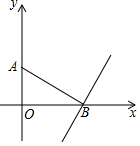 如图,点A(0,3),B(6,0),过点B作AB的垂线l.若直线l上存在点C,满足BC=2$\sqrt{5}$,则点C的坐标为(8,4)或(4,-4).
如图,点A(0,3),B(6,0),过点B作AB的垂线l.若直线l上存在点C,满足BC=2$\sqrt{5}$,则点C的坐标为(8,4)或(4,-4). 如图,在△ABC中,AD是∠BAC的平分线,E,F分别为AB,AC上的点,若DE=DF,且AE>AF,求证:∠EDF与∠BAF互补(提示:作DM⊥AB于点M,DN⊥AC于点N)
如图,在△ABC中,AD是∠BAC的平分线,E,F分别为AB,AC上的点,若DE=DF,且AE>AF,求证:∠EDF与∠BAF互补(提示:作DM⊥AB于点M,DN⊥AC于点N)