题目内容
16.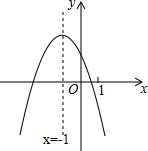 二次函数y=ax2+bx+c(a≠0)的图象如图,下列结论正确的是( )
二次函数y=ax2+bx+c(a≠0)的图象如图,下列结论正确的是( )| A. | 2a-b=0 | B. | b>0 | C. | a+b+c>0 | D. | 4a-2b+c<0 |
分析 由抛物线的开口方向判断a与0的关系,由抛物线的对称轴得出a与b关系,然后根据x=1和x=-2进行推理,进而对所得结论进行判断.
解答 解:∵抛物线开口向下,
∴a<0,
∵对称轴为直线x=-1,
∴-$\frac{b}{2a}$=-1,b<0,故B错误;
∴2a-b=0,故A正确;
当x=1时,y=a+b+c<0,故C错误;
当x=-2时,y=4a-2b+c>0,故D错误;
故选A.
点评 本题考查了图象与二次函数系数之间的关系,会利用对称轴的范围求2a与b的关系,以及二次函数与方程之间的转换,根的判别式的熟练运用.

练习册系列答案
相关题目
9.如果一个多边形的每个内角都相等,且内角和为1260°,那么这个多边形的一个外角等于( )
| A. | 30° | B. | 36° | C. | 40° | D. | 45° |
4.下列各运算中,正确的是( )
| A. | a2+a3=a5 | B. | (a+1)2=a2+1 | C. | $\sqrt{a}$•$\sqrt{b}$=$\sqrt{ab}$ | D. | $\sqrt{2}$+$\sqrt{3}$=$\sqrt{5}$ |
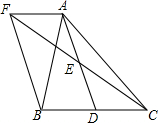 如图,在△ABC中,D是BC边上的一点,E是AD的中点,过A点作BC的平行线交CE的延长线于点F,且AF=BD,连接BF.
如图,在△ABC中,D是BC边上的一点,E是AD的中点,过A点作BC的平行线交CE的延长线于点F,且AF=BD,连接BF. 如图,线段AB的长为l.
如图,线段AB的长为l.