题目内容
5. 如图,线段AB的长为l.
如图,线段AB的长为l.(1)线段AB上的点C满足关系式AC2=BC•AB,求线段AC的长度;
(2)线段AC上的点D满足关系式AD2=CD•AC,求线段AD的长度;
(3)线段AD上的点E满足关系式AE2=DE•AD,求线段AE的长度.
分析 (1)设AC=x,则BC=AB-AC=1-x,x2=1×(1-x),整理得x2+x-1=0,然后解方程即可;
(2)设线段AD的长度为x,AC=l,则x2=l×(l-x),然后解方程;
(3)与(2)的解法一样.
解答 解:(1)设AC=x,则BC=AB-AC=1-x,
∵AC2=BC•AB,
∴x2=1×(1-x),
整理得x2+x-1=0,
解得${x}_{1}=\frac{\sqrt{5}-1}{2}$,${x}_{2}=\frac{-\sqrt{5}-1}{2}$(舍去),
所以线段AC的长度为$\frac{\sqrt{5}-1}{2}$;
(2)设线段AD的长度为x,AC=l,
∵AD2=CD•AC,
∴x2=l×(l-x),
∴${x}_{1}=\frac{-1+\sqrt{5}}{2}$,${x}_{2}=\frac{-1-\sqrt{5}}{2}$(舍去),
∴线段AD的长度$\frac{\sqrt{5}-1}{2}$AC;
(3)同理得到线段AE的长度为$\frac{\sqrt{5}-1}{2}$AD.
点评 本题考查了黄金分割:把线段AB分成两条线段AC和BC(AC>BC),且使AC是AB和BC的比例中项(即AB:AC=AC:BC),叫做把线段AB黄金分割,点C叫做线段AB的黄金分割点;其中AC=$\frac{\sqrt{5}-1}{2}$AB≈0.618AB,并且线段AB的黄金分割点有两个.

练习册系列答案
相关题目
15.某校准备组织520名学生进行野外考察活动,行李共有240件.学校计划租用甲、乙两种型号的汽车共12辆,经了解,甲种汽车每辆最多能载50人和15件行李,乙种汽车每辆最多能载40人和25件行李.设租用甲种汽车x辆,你认为下列符合题意的不等式组是( )
| A. | $\left\{\begin{array}{l}{50x+40(12-x)≥520}\\{15x+25(12-x)≥240}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{50x+40(12-x)>520}\\{15x+25(12-x)>240}\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}{50x+40(12-x)≤520}\\{15x+25(12-x)≤240}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{50x+40(12-x)<520}\\{15x+25(12-x)<240}\end{array}\right.$ |
16.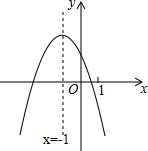 二次函数y=ax2+bx+c(a≠0)的图象如图,下列结论正确的是( )
二次函数y=ax2+bx+c(a≠0)的图象如图,下列结论正确的是( )
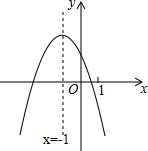 二次函数y=ax2+bx+c(a≠0)的图象如图,下列结论正确的是( )
二次函数y=ax2+bx+c(a≠0)的图象如图,下列结论正确的是( )| A. | 2a-b=0 | B. | b>0 | C. | a+b+c>0 | D. | 4a-2b+c<0 |
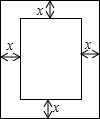 已知一长方形打印纸长20厘米,宽15厘米,现在要打印纸上打印文稿,上下左右个留出一定距离,设留出的距离均为xcm,打印文稿面积为y(如图).写出y与x的关系式,并求出x的取值范围.
已知一长方形打印纸长20厘米,宽15厘米,现在要打印纸上打印文稿,上下左右个留出一定距离,设留出的距离均为xcm,打印文稿面积为y(如图).写出y与x的关系式,并求出x的取值范围.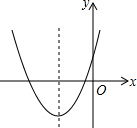 抛物线y=ax2+bx+c中,b=4a,它的图象如图,有以下结论:①c>0;②a+b+c>0;③a-b+c>0;④b2-4ac<0;⑤abc<0;⑥4a>c;其中正确的为( )
抛物线y=ax2+bx+c中,b=4a,它的图象如图,有以下结论:①c>0;②a+b+c>0;③a-b+c>0;④b2-4ac<0;⑤abc<0;⑥4a>c;其中正确的为( )