题目内容
1．先化简，再求值：$\frac{{x}^{2}+2x+1}{2x-6}$÷（x-$\frac{1-3x}{x-3}$），其中x为方程（x-3）（x-5）=0的根．分析 先根据分式混合运算的法则把原式进行化简，再求x的值，代入原式进行计算即可．
解答 解：原式=$\frac{（x+1）^{2}}{2（x-3）}$÷$\frac{x（x-3）-1+3x}{x-3}$
=$\frac{{（x+1）}^{2}}{2（x-3）}$•$\frac{x-3}{（x+1）（x-1）}$
=$\frac{x+1}{2（x-1）}$，
∵x为方程（x-3）（x-5）=0的根，
∴x1=3，x2=5，
∵当x=3时分式无意义，
∴当x=5时，原式=$\frac{5+1}{2（5-1）}$=$\frac{3}{4}$．
点评 本题考查的是分式的化简求值，熟知分式混合运算的法则是解答此题的关键．
练习册系列答案
王后雄学案教材完全解读系列答案
海淀课时新作业金榜卷系列答案
相关题目
16．
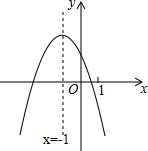二次函数y=ax2+bx+c（a≠0）的图象如图，下列结论正确的是（ ）
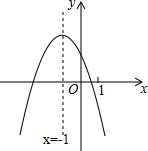二次函数y=ax2+bx+c（a≠0）的图象如图，下列结论正确的是（ ）| A． | 2a-b=0 | B． | b＞0 | C． | a+b+c＞0 | D． | 4a-2b+c＜0 |