题目内容
11.先化简(1-$\frac{1}{m+3}$)÷$\frac{{m}^{2}-4}{{m}^{2}-9}$,再从|m|≤2中选一个合适的整数代入求值.分析 先根据分式混合运算的法则把原式进行化简,再选出合适的m的值代入进行计算即可.
解答 解:原式=$\frac{m+2}{m+3}$•$\frac{(m+3)(m-3)}{(m+2)(m-2)}$
=$\frac{m-3}{m-2}$,
∵|m|≤2,
∴取m=1,
原式=2.
点评 本题考查的是分式的化简求值,熟知分式混合运算的法则是解答此题的关键.

练习册系列答案
相关题目
2. 如图把两个不等式的解集表示在数轴上,则这两个不等式组成的不等式组可能是( )
如图把两个不等式的解集表示在数轴上,则这两个不等式组成的不等式组可能是( )
 如图把两个不等式的解集表示在数轴上,则这两个不等式组成的不等式组可能是( )
如图把两个不等式的解集表示在数轴上,则这两个不等式组成的不等式组可能是( )| A. | $\left\{\begin{array}{l}{x<4}\\{x≥-1}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x>4}\\{x≤1}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x>4}\\{x>-1}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x≤4}\\{x>-1}\end{array}\right.$ |
19. 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列5个结论:
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列5个结论:
①abc<0;
②a-b+c>0;
③4a+2b+c>0;
④b<-2a;
⑤a+b+c>am2+bm+c(m≠1的实数)
其中正确的结论有( )
 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列5个结论:
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列5个结论:①abc<0;
②a-b+c>0;
③4a+2b+c>0;
④b<-2a;
⑤a+b+c>am2+bm+c(m≠1的实数)
其中正确的结论有( )
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
6. 如图,m∥n,∠1+∠2=80°,则∠3+∠4的度数为( )
如图,m∥n,∠1+∠2=80°,则∠3+∠4的度数为( )
 如图,m∥n,∠1+∠2=80°,则∠3+∠4的度数为( )
如图,m∥n,∠1+∠2=80°,则∠3+∠4的度数为( )| A. | 60° | B. | 80° | C. | 100° | D. | 120° |
16.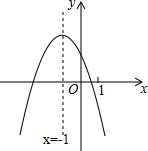 二次函数y=ax2+bx+c(a≠0)的图象如图,下列结论正确的是( )
二次函数y=ax2+bx+c(a≠0)的图象如图,下列结论正确的是( )
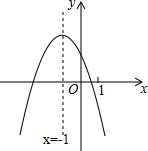 二次函数y=ax2+bx+c(a≠0)的图象如图,下列结论正确的是( )
二次函数y=ax2+bx+c(a≠0)的图象如图,下列结论正确的是( )| A. | 2a-b=0 | B. | b>0 | C. | a+b+c>0 | D. | 4a-2b+c<0 |
3.下列运算中,结果是a6的是( )
| A. | a2•a3 | B. | a12÷a2 | C. | (a3)3 | D. | (-a)6 |