题目内容
4．下列各运算中，正确的是（ ）| A． | a2+a3=a5 | B． | （a+1）2=a2+1 | C． | $\sqrt{a}$•$\sqrt{b}$=$\sqrt{ab}$ | D． | $\sqrt{2}$+$\sqrt{3}$=$\sqrt{5}$ |
分析 根据同底数幂的乘法、完全平方公式、二次根式的性质，乘法，即可解答．
解答 解：A、a2•a3=a5，故错误；
B、（a+1）2=a2+2a+1，故错误；
C、正确；
D、$\sqrt{2}$与$\sqrt{3}$不是同类二次根式，不能合并，故错误；
故选：C．
点评 本题考查了完全平方公式、二次根式的乘法，解决本题的关键是熟记二次根式的性质，完全平方公式．
练习册系列答案
相关题目
如图，求∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H的度数．
15．某校准备组织520名学生进行野外考察活动，行李共有240件．学校计划租用甲、乙两种型号的汽车共12辆，经了解，甲种汽车每辆最多能载50人和15件行李，乙种汽车每辆最多能载40人和25件行李．设租用甲种汽车x辆，你认为下列符合题意的不等式组是（ ）
| A． | $\left\{\begin{array}{l}{50x+40（12-x）≥520}\\{15x+25（12-x）≥240}\end{array}\right.$ | B． | $\left\{\begin{array}{l}{50x+40（12-x）＞520}\\{15x+25（12-x）＞240}\end{array}\right.$ | ||
| C． | $\left\{\begin{array}{l}{50x+40（12-x）≤520}\\{15x+25（12-x）≤240}\end{array}\right.$ | D． | $\left\{\begin{array}{l}{50x+40（12-x）＜520}\\{15x+25（12-x）＜240}\end{array}\right.$ |
19．
已知二次函数y=ax2+bx+c（a≠0）的图象如图所示，有下列5个结论：
①abc＜0；
②a-b+c＞0；
③4a+2b+c＞0；
④b＜-2a；
⑤a+b+c＞am2+bm+c（m≠1的实数）
其中正确的结论有（ ）
已知二次函数y=ax2+bx+c（a≠0）的图象如图所示，有下列5个结论：①abc＜0；
②a-b+c＞0；
③4a+2b+c＞0；
④b＜-2a；
⑤a+b+c＞am2+bm+c（m≠1的实数）
其中正确的结论有（ ）
| A． | 2个 | B． | 3个 | C． | 4个 | D． | 5个 |
16．
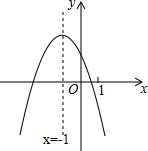二次函数y=ax2+bx+c（a≠0）的图象如图，下列结论正确的是（ ）
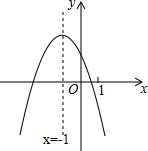二次函数y=ax2+bx+c（a≠0）的图象如图，下列结论正确的是（ ）| A． | 2a-b=0 | B． | b＞0 | C． | a+b+c＞0 | D． | 4a-2b+c＜0 |
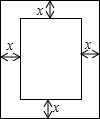已知一长方形打印纸长20厘米，宽15厘米，现在要打印纸上打印文稿，上下左右个留出一定距离，设留出的距离均为xcm，打印文稿面积为y（如图）．写出y与x的关系式，并求出x的取值范围．