题目内容
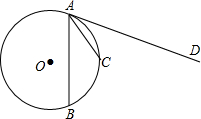如图，AB、AC是⊙O的弦，AD是⊙O的切线，且AC平分∠BAD， |
| AC |
|
| BC |
考点：切线的性质
专题：计算题
分析：作直径AE，连结CE、CB，如图，根据切线的性质得AE⊥AD，则∠1+∠EAC=90°，再根据圆周角定理，由AE为直径得∠ACE=90°，则利用等角的余角相等得到∠1=∠E，而由圆周角定理得到∠E=∠B，由AC平分∠BAD得到∠1=∠2，所以∠B=∠2，于是根据圆周角定理即可得到
=
．
|
| AC |
|
| BC |
解答：解：作直径AE，连结CE、CB，如图，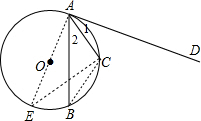
∵AD是⊙O的切线，
∴AE⊥AD，
∴∠1+∠EAC=90°，
∵AE为直径，
∴∠ACE=90°，
∴∠EAC+∠E=90°，
∴∠1=∠E，
而∠E=∠B，
∴∠B=∠1，
∵AC平分∠BAD，
∴∠1=∠2，
∴∠B=∠2，
∴
=
．
∵AD是⊙O的切线，
∴AE⊥AD，
∴∠1+∠EAC=90°，
∵AE为直径，
∴∠ACE=90°，
∴∠EAC+∠E=90°，
∴∠1=∠E，
而∠E=∠B，
∴∠B=∠1，
∵AC平分∠BAD，
∴∠1=∠2，
∴∠B=∠2，
∴
|
| AC |
|
| BC |
点评：本题考查了切线的性质：圆的切线垂直于经过切点的半径．也考查了圆周角定理．
练习册系列答案
相关题目
M、N是⊙O上两点，已知OM=4cm，那么一定有（ ）
| A、MN＞8cm |
| B、MN=8cm |
| C、MN＜8cm |
| D、MN≤8cm |
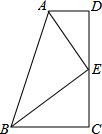如图，已知四边形ABCD中，∠D=∠C=90°，AE平分∠BAD，点E是DC的中点，且E在DC上．
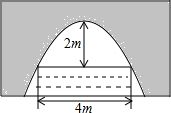有一座抛物线形拱桥，正常水位时桥下水面宽度为4m，拱顶距离水面 2m．
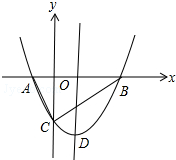如图，抛物线y=x2+bx-2与x轴交于A，B两点，与y轴交于C点，且A（-1，0）．