题目内容
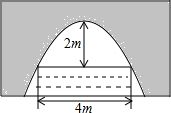 有一座抛物线形拱桥,正常水位时桥下水面宽度为4m,拱顶距离水面 2m.
有一座抛物线形拱桥,正常水位时桥下水面宽度为4m,拱顶距离水面 2m.(1)求出这条抛物线表示的函数的解析式;
(2)设正常水位时桥下的水深为2m,为保证过往船只顺利航行,桥下水面的宽度不得小于2m.求水深超过多少m时就会影响过往船只在桥下顺利航行.
考点:二次函数的应用
专题:
分析:(1)以桥拱的顶点为原点建立平面直角坐标系,如图,设抛物线的解析式为y=ax2,由待定系数法求出其解即可.
(2)当水面的宽度为2m时,把x=1代入解析式就可以求出y的值,由2-0.5就可以求出水上升的高度,进而求出水的深度.
(2)当水面的宽度为2m时,把x=1代入解析式就可以求出y的值,由2-0.5就可以求出水上升的高度,进而求出水的深度.
解答:解:(1)以桥拱的顶点为原点建立平面直角坐标系,设这条抛物线表示的函数的解析式为:y=ax2,由图象,得
-2=4a,
解得:a=-
,
故抛物线表示的函数的解析式为:y=-
x2;
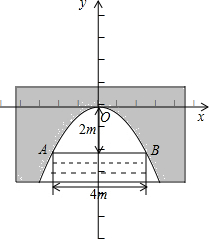
(2)由题意,得
当x=1时 y=-0.5
-0.5-(-4)=3.5(m)
答:水深超过3.5m 时就会影响过往船只在桥下顺利航行.
-2=4a,
解得:a=-
| 1 |
| 2 |
故抛物线表示的函数的解析式为:y=-
| 1 |
| 2 |

(2)由题意,得
当x=1时 y=-0.5
-0.5-(-4)=3.5(m)
答:水深超过3.5m 时就会影响过往船只在桥下顺利航行.
点评:本题考查了待定系数法求二次函数的解析式的运用,运用二次函数解实际问题的运用,解答时求出函数的解析式是关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
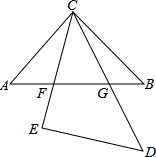 如图是两块等腰直角三角板放置在一起,AC=BC,∠ACB=90°,CE=DE,∠E=90°,CE交AB于F,CD交AB于G.求证:AF2+BG2=FG2.
如图是两块等腰直角三角板放置在一起,AC=BC,∠ACB=90°,CE=DE,∠E=90°,CE交AB于F,CD交AB于G.求证:AF2+BG2=FG2.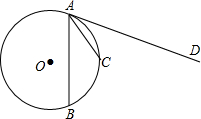 如图,AB、AC是⊙O的弦,AD是⊙O的切线,且AC平分∠BAD,
如图,AB、AC是⊙O的弦,AD是⊙O的切线,且AC平分∠BAD,
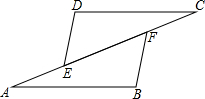 如图,AB∥CD,AE=CF,AB=CD.求证:DE=BF.
如图,AB∥CD,AE=CF,AB=CD.求证:DE=BF.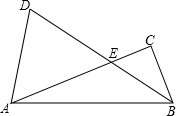 在Rt△ABC中,∠C=90°,∠CAB=α,边AB绕点B按顺时针方向旋转2α得到DB,交AC边点E,连接AD,当
在Rt△ABC中,∠C=90°,∠CAB=α,边AB绕点B按顺时针方向旋转2α得到DB,交AC边点E,连接AD,当