题目内容
已知正三角形的边长为a,求其内切圆的內接正方形的面积.
考点:三角形的内切圆与内心
专题:
分析:根据等边三角形的三线合一,可以构造一个由其内切圆的半径、外接圆的半径和半边组成的30°的直角三角形,利用锐角三角函数关系求出内切圆半径,即可求得正方形的对角线长,进而求得面积.
解答: 解:∵内切圆的半径、外接圆的半径和半边组成一个30°的直角三角形,
解:∵内切圆的半径、外接圆的半径和半边组成一个30°的直角三角形,
则∠OBD=30°,BD=
,
∴tan∠BOD=
=
,
∴内切圆半径OD=
×
=
a.
则内切圆的直径长是
a,
则内接正方形的面积是:
×(
a)2=
a2.
 解:∵内切圆的半径、外接圆的半径和半边组成一个30°的直角三角形,
解:∵内切圆的半径、外接圆的半径和半边组成一个30°的直角三角形,则∠OBD=30°,BD=
| a |
| 2 |
∴tan∠BOD=
| OD |
| BD |
| ||
| 3 |
∴内切圆半径OD=
| ||
| 3 |
| a |
| 2 |
| ||
| 6 |
则内切圆的直径长是
| ||
| 3 |
则内接正方形的面积是:
| 1 |
| 2 |
| ||
| 3 |
| 1 |
| 6 |
点评:此题主要考查了三角形的内切圆,注意:根据等边三角形的三线合一,可以发现其内切圆的半径、外接圆的半径和半边正好组成了一个30°的直角三角形.

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案
相关题目
多项式4n-2n2+2+6n2减去3(n2+2n3-1+3n)(n为自然数)的差一定是( )
| A、奇数 | B、偶数 |
| C、5的倍数 | D、以上答案都不对 |
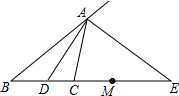 已知:AD、AE分别是△ABC的内外角平分线,M为DE中点,求证:
已知:AD、AE分别是△ABC的内外角平分线,M为DE中点,求证: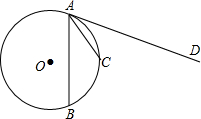 如图,AB、AC是⊙O的弦,AD是⊙O的切线,且AC平分∠BAD,
如图,AB、AC是⊙O的弦,AD是⊙O的切线,且AC平分∠BAD,