题目内容
若关于x的一元二次方程kx2+2x+1=0有两个实数根，则k的取值范围是 ．
考点：根的判别式,一元二次方程的定义
专题：
分析：若一元二次方程有两不等实数根，则根的判别式△=b2-4ac≥0，建立关于k的不等式，求出k的取值范围．还要注意二次项系数不为0．
解答：解：∵关于x的一元二次方程kx2+2x+1=0有两个实数根，
∴根的判别式△=b2-4ac=4-4k≥0，且k≠0．
即k≤1且k≠0．
故答案是：k≤1且k≠0．
∴根的判别式△=b2-4ac=4-4k≥0，且k≠0．
即k≤1且k≠0．
故答案是：k≤1且k≠0．
点评：本题考查了一元二次方程根的判别式的应用．切记不要忽略一元二次方程二次项系数不为零这一隐含条件．
练习册系列答案
相关题目
下列实数中，无理数有（ ）
，-
，-
，|-1|，
，
，0.1010010001…（相邻两个1之间的0的个数依次增加1）
| 1 |
| 2 |
| 16 |
| π |
| 3 |
| 22 |
| 7 |
| 9 |
| A、1个 | B、2个 | C、3个 | D、4个 |
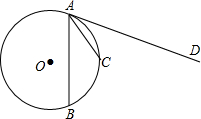如图，AB、AC是⊙O的弦，AD是⊙O的切线，且AC平分∠BAD，
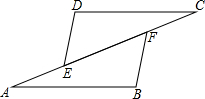如图，AB∥CD，AE=CF，AB=CD．求证：DE=BF．
文明餐桌，拒绝“剩”宴！某中学发起“拒绝浪费，从我做起”的“光盘”行动！学校为了了解学生生活习惯是否符合“光盘”观念，在全校进行了一次问卷调查，若学生生活习惯符合“关盘”观念，则称其为“光盘族”；否则，称其为“非光盘族”．学校有七、八、九三个年级，经过统计，将全校的“光盘族”人数按年级绘制成如两幅统计图：
如图是由六个棱长为1的小正方体组成的几何体，其俯视图的面积是