题目内容
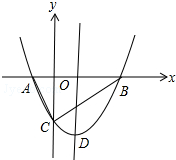 如图,抛物线y=x2+bx-2与x轴交于A,B两点,与y轴交于C点,且A(-1,0).
如图,抛物线y=x2+bx-2与x轴交于A,B两点,与y轴交于C点,且A(-1,0).(1)求抛物线的函数关系式及顶点D的坐标;
(2)若点M是抛物线对称轴上的一个动点,求CM+AM的最小值.
考点:抛物线与x轴的交点,轴对称-最短路线问题
专题:
分析:(1)把A的坐标代入函数的解析式,即可求得b的值,然后利用配方法即可求得顶点坐标;
(2)直线BC与抛物线的对称轴的交点就是使CM+AM取得最小值的M的点,BC的长就是最小值.
(2)直线BC与抛物线的对称轴的交点就是使CM+AM取得最小值的M的点,BC的长就是最小值.
解答:解:(1)∵点A(-1,0)在抛物线y=x2+bx-2上,
∴b=-1,
∴抛物线解析式y=x2-x-2,
∵抛物线y=x2-x-2=(x-
)2-
,
∴顶点D的坐标(
,-
);
(2)当x=0时,y=-2,
∴C(0,-2),
∴OC=2,
当y=0时,0=x2-x-2,解得:x=2或-1,
∴B(2,0),
∴OB=2,
由抛物线的性质可知:点A和B是对称点,
∴AM=BM,
∴AM+CM=BM+CM≥BC=2
.
∴CM+AM的最小值是2
.
∴b=-1,
∴抛物线解析式y=x2-x-2,
∵抛物线y=x2-x-2=(x-
| 1 |
| 2 |
| 9 |
| 4 |
∴顶点D的坐标(
| 1 |
| 2 |
| 9 |
| 4 |
(2)当x=0时,y=-2,
∴C(0,-2),
∴OC=2,
当y=0时,0=x2-x-2,解得:x=2或-1,
∴B(2,0),
∴OB=2,
由抛物线的性质可知:点A和B是对称点,
∴AM=BM,
∴AM+CM=BM+CM≥BC=2
| 2 |
∴CM+AM的最小值是2
| 2 |
点评:本题考查了利用配方法确定二次函数的顶点坐标以及对称点的作法,正确确定直线BC与抛物线的对称轴的交点就是使CM+AM取得最小值的M的点,是关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
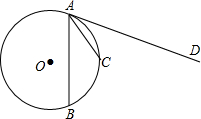 如图,AB、AC是⊙O的弦,AD是⊙O的切线,且AC平分∠BAD,
如图,AB、AC是⊙O的弦,AD是⊙O的切线,且AC平分∠BAD,
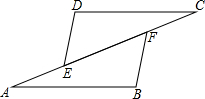 如图,AB∥CD,AE=CF,AB=CD.求证:DE=BF.
如图,AB∥CD,AE=CF,AB=CD.求证:DE=BF. 文明餐桌,拒绝“剩”宴!某中学发起“拒绝浪费,从我做起”的“光盘”行动!学校为了了解学生生活习惯是否符合“光盘”观念,在全校进行了一次问卷调查,若学生生活习惯符合“关盘”观念,则称其为“光盘族”;否则,称其为“非光盘族”.学校有七、八、九三个年级,经过统计,将全校的“光盘族”人数按年级绘制成如两幅统计图:
文明餐桌,拒绝“剩”宴!某中学发起“拒绝浪费,从我做起”的“光盘”行动!学校为了了解学生生活习惯是否符合“光盘”观念,在全校进行了一次问卷调查,若学生生活习惯符合“关盘”观念,则称其为“光盘族”;否则,称其为“非光盘族”.学校有七、八、九三个年级,经过统计,将全校的“光盘族”人数按年级绘制成如两幅统计图: