题目内容
计算：
（1）（a-2b+1）（a+2b-1）
（2）（x-y-z）2．
（1）（a-2b+1）（a+2b-1）
（2）（x-y-z）2．
考点：完全平方公式,平方差公式
专题：
分析：（1）先变形得出[a-（2b-1）][a+（2b-1）]，再根据平方差公式进行计算，最后根据完全平方公式求出即可；
（2）首先把x-y-z看作（x-y）-z，利用完全平方公式展开，再进一步利用整式的乘法和完全平方公式继续计算即可．
（2）首先把x-y-z看作（x-y）-z，利用完全平方公式展开，再进一步利用整式的乘法和完全平方公式继续计算即可．
解答：解：（1）（a-2b+1）（a+2b-1）
=[a-（2b-1）][a+（2b-1）]
=a2-（2b-1）2
=a2-4b2+4b-1；
（2）（x-y-z）2
=[（x-y）-z]2
=（x-y）2-2（x-y）z+z2
=x2-2xy+y2-2xz+2yz+z2．
=[a-（2b-1）][a+（2b-1）]
=a2-（2b-1）2
=a2-4b2+4b-1；
（2）（x-y-z）2
=[（x-y）-z]2
=（x-y）2-2（x-y）z+z2
=x2-2xy+y2-2xz+2yz+z2．
点评：本题考查了平方差公式和完全平方公式的应用，主要考查学生运用公式进行推理和计算的能力．
练习册系列答案
名校课堂系列答案
相关题目
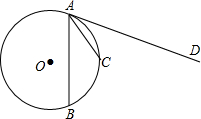如图，AB、AC是⊙O的弦，AD是⊙O的切线，且AC平分∠BAD，
文明餐桌，拒绝“剩”宴！某中学发起“拒绝浪费，从我做起”的“光盘”行动！学校为了了解学生生活习惯是否符合“光盘”观念，在全校进行了一次问卷调查，若学生生活习惯符合“关盘”观念，则称其为“光盘族”；否则，称其为“非光盘族”．学校有七、八、九三个年级，经过统计，将全校的“光盘族”人数按年级绘制成如两幅统计图：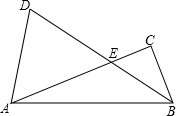
在Rt△ABC中，∠C=90°，∠CAB=α，边AB绕点B按顺时针方向旋转2α得到DB，交AC边点E，连接AD，当
如图是由六个棱长为1的小正方体组成的几何体，其俯视图的面积是