题目内容
等腰△ABC中,AB=AC=5,BC=6,AD是BC边上的高线,M是AD上的动点,E是AB上的一动点,求EM+BM的最小值.
考点:轴对称-最短路线问题,等腰三角形的性质
专题:
分析:作E关于AD的对称点E′,连接BE′交AD于M,连接EM,过B作BF⊥AC于F,根据三线合一定理求出BD的长,根据勾股定理求出AD,根据三角形面积公式求出BF,根据对称性质求出BM+EM=BE,根据垂线段最短得出BM+EM≥
,即可得出答案.
| 24 |
| 5 |
解答: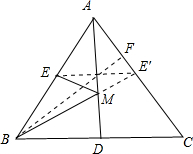 解:作E关于AD的对称点E′,连接BE′交AD于M,连接EM,过B作BF⊥AC于F,
解:作E关于AD的对称点E′,连接BE′交AD于M,连接EM,过B作BF⊥AC于F,
∵AB=AC=5,BC=6,AD是BC边上的高线,
∴BD=DC=3,AD平分∠BAC,
∴E′在AC上,
在Rt△ABD中,由勾股定理得:AD=
=4,
∴S△ABC=
×BC×AD=
×AC×BF,
∴BF=
=
=
,
∵E关于AD的对称点E′,
∴EM=E′M,
∴BM+EM=BM+E′M=BE′,
根据垂线段最短得出:BE′≥BF,
即BM+EM≥
,
即BM+EM的最小值是
.
 解:作E关于AD的对称点E′,连接BE′交AD于M,连接EM,过B作BF⊥AC于F,
解:作E关于AD的对称点E′,连接BE′交AD于M,连接EM,过B作BF⊥AC于F,∵AB=AC=5,BC=6,AD是BC边上的高线,
∴BD=DC=3,AD平分∠BAC,
∴E′在AC上,
在Rt△ABD中,由勾股定理得:AD=
| 52-32 |
∴S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
∴BF=
| BC×AD |
| AC |
| 6×4 |
| 5 |
| 24 |
| 5 |
∵E关于AD的对称点E′,
∴EM=E′M,
∴BM+EM=BM+E′M=BE′,
根据垂线段最短得出:BE′≥BF,
即BM+EM≥
| 24 |
| 5 |
即BM+EM的最小值是
| 24 |
| 5 |
点评:本题考查了轴对称-最短路线问题,关键是画出符合条件的图形,题目具有一定的代表性,是一道比较好的题目.

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
下列实数中,无理数有( )
,-
,-
,|-1|,
,
,0.1010010001…(相邻两个1之间的0的个数依次增加1)
| 1 |
| 2 |
| 16 |
| π |
| 3 |
| 22 |
| 7 |
| 9 |
| A、1个 | B、2个 | C、3个 | D、4个 |
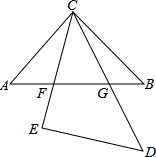 如图是两块等腰直角三角板放置在一起,AC=BC,∠ACB=90°,CE=DE,∠E=90°,CE交AB于F,CD交AB于G.求证:AF2+BG2=FG2.
如图是两块等腰直角三角板放置在一起,AC=BC,∠ACB=90°,CE=DE,∠E=90°,CE交AB于F,CD交AB于G.求证:AF2+BG2=FG2.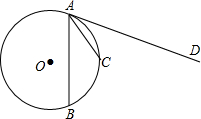 如图,AB、AC是⊙O的弦,AD是⊙O的切线,且AC平分∠BAD,
如图,AB、AC是⊙O的弦,AD是⊙O的切线,且AC平分∠BAD,
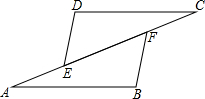 如图,AB∥CD,AE=CF,AB=CD.求证:DE=BF.
如图,AB∥CD,AE=CF,AB=CD.求证:DE=BF.