题目内容
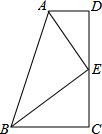 如图,已知四边形ABCD中,∠D=∠C=90°,AE平分∠BAD,点E是DC的中点,且E在DC上.
如图,已知四边形ABCD中,∠D=∠C=90°,AE平分∠BAD,点E是DC的中点,且E在DC上.(1)求证:BE平分∠ABC;
(2)求∠AEB;
(3)求证:AD+BC=AB.
考点:全等三角形的判定与性质,角平分线的性质
专题:
分析:(1)过E作EF⊥AB于F,根据角平分线性质得出EF=DE,推出EF=CE,根据角平分线性质得出即可;
(2)延长AE、BC交于点M,求出∠DAE=∠CME,AB=BM,根据ASA推出△ADE≌△MCE,根据全等得出AE=EM,∠DAE=∠M,求出∠M=∠BAE,推出AB=BM,根据等腰三角形的性质得出即可;
(3)根据全等三角形的性质得出AD=CM,即可得出答案.
(2)延长AE、BC交于点M,求出∠DAE=∠CME,AB=BM,根据ASA推出△ADE≌△MCE,根据全等得出AE=EM,∠DAE=∠M,求出∠M=∠BAE,推出AB=BM,根据等腰三角形的性质得出即可;
(3)根据全等三角形的性质得出AD=CM,即可得出答案.
解答:
(1)证明:过E作EF⊥AB于F,
∵∠D=90°,AE平分∠BAD,
∴EF=DE,
∵E为DC中点,
∴DE=EC,
∴EF=EC,
∵EF⊥AB,∠C=90°,
∴BE平分∠ABC;
(2)解:延长AE、BC交于点M,
∵AD∥BC
∴∠DAE=∠CME,
∵AE平分∠BAD,
∴∠DAE=∠BAM,
∴∠BAM=∠CME,
∴AB=BM,
在△ADE和△MCE中
∴△ADE≌△MCE,
∴AE=EM,∠DAE=∠M
∵AE平分∠BAD,
∴∠DAE=∠BAE,
∴∠M=∠BAE,
∴AB=BM,
∵AE=EM,
∴BE⊥AM,
∴∠AEB=90°;
(3)证明:∵△ADE≌△MCE,
∴AD=CM,
∵AB=BM,BM=BC+CM,
∴AD+BC=AB.

(1)证明:过E作EF⊥AB于F,
∵∠D=90°,AE平分∠BAD,
∴EF=DE,
∵E为DC中点,
∴DE=EC,
∴EF=EC,
∵EF⊥AB,∠C=90°,
∴BE平分∠ABC;
(2)解:延长AE、BC交于点M,

∵AD∥BC
∴∠DAE=∠CME,
∵AE平分∠BAD,
∴∠DAE=∠BAM,
∴∠BAM=∠CME,
∴AB=BM,
在△ADE和△MCE中
|
∴△ADE≌△MCE,
∴AE=EM,∠DAE=∠M
∵AE平分∠BAD,
∴∠DAE=∠BAE,
∴∠M=∠BAE,
∴AB=BM,
∵AE=EM,
∴BE⊥AM,
∴∠AEB=90°;
(3)证明:∵△ADE≌△MCE,
∴AD=CM,
∵AB=BM,BM=BC+CM,
∴AD+BC=AB.
点评:本题主要考查了全等三角形的判定与性质及等腰三角形的性质,全等三角形的判定是结合全等三角形的性质证明线段和角相等的重要工具.在判定三角形全等时,关键是选择恰当的判定条件.

练习册系列答案
相关题目
在
,3.14,0.3131131113,π,
,1.
,-
,
中无理数的个数有( )
| 4 |
| 10 |
| •• |
| 51 |
| 0.001 |
| 2 |
| 7 |
| A、2个 | B、3个 | C、4个 | D、5个 |
下列实数中,无理数有( )
,-
,-
,|-1|,
,
,0.1010010001…(相邻两个1之间的0的个数依次增加1)
| 1 |
| 2 |
| 16 |
| π |
| 3 |
| 22 |
| 7 |
| 9 |
| A、1个 | B、2个 | C、3个 | D、4个 |
多项式4n-2n2+2+6n2减去3(n2+2n3-1+3n)(n为自然数)的差一定是( )
| A、奇数 | B、偶数 |
| C、5的倍数 | D、以上答案都不对 |
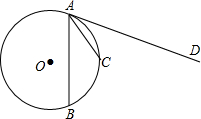 如图,AB、AC是⊙O的弦,AD是⊙O的切线,且AC平分∠BAD,
如图,AB、AC是⊙O的弦,AD是⊙O的切线,且AC平分∠BAD,
 文明餐桌,拒绝“剩”宴!某中学发起“拒绝浪费,从我做起”的“光盘”行动!学校为了了解学生生活习惯是否符合“光盘”观念,在全校进行了一次问卷调查,若学生生活习惯符合“关盘”观念,则称其为“光盘族”;否则,称其为“非光盘族”.学校有七、八、九三个年级,经过统计,将全校的“光盘族”人数按年级绘制成如两幅统计图:
文明餐桌,拒绝“剩”宴!某中学发起“拒绝浪费,从我做起”的“光盘”行动!学校为了了解学生生活习惯是否符合“光盘”观念,在全校进行了一次问卷调查,若学生生活习惯符合“关盘”观念,则称其为“光盘族”;否则,称其为“非光盘族”.学校有七、八、九三个年级,经过统计,将全校的“光盘族”人数按年级绘制成如两幅统计图: