题目内容
6. 如图,在4×4的正方形方格中,△ABC和△DEF的顶点都在边长为1的小正方形的顶点上.
如图,在4×4的正方形方格中,△ABC和△DEF的顶点都在边长为1的小正方形的顶点上.(1)填空:∠ABC=135°,AC=2$\sqrt{5}$;
(2)判断:△ABC与△DEF是否相似,并证明你的结论.
分析 (1)先在Rt△BCG中根据等腰直角三角形的性质求出∠GBC的度数,再根据∠ABC=∠GBC+∠ABG即可得出∠ABC的度数;在Rt△ACH中利用勾股定理即可求出AC的长;
(2)根据相似三角形的判定定理,夹角相等,对应边成比例即可证明△ABC与△DEF相似.
解答 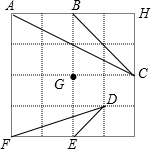 解:(1)∵△BCG是等腰直角三角形,
解:(1)∵△BCG是等腰直角三角形,
∴∠GBC=45°,
∵∠ABG=90°,
∴∠ABC=∠GBC+∠ABG=90°+45°=135°;
∵在Rt△AHC中,AH=4,CH=2,
∴AC=$\sqrt{A{H}^{2}+C{H}^{2}}$=$\sqrt{{4}^{2}+{2}^{2}}$=2$\sqrt{5}$.
故答案为:135,$2\sqrt{5}$;
(2)△ABC∽△DEF.
证明:∵在4×4的正方形方格中,
∠ABC=∠DEF=135°,
∴∠ABC=∠DEF.
∵AB=2,BC=2$\sqrt{2}$,FE=2,DE=$\sqrt{2}$,
∴$\frac{AB}{DE}$=$\frac{2}{\sqrt{2}}$=$\sqrt{2}$,$\frac{BC}{EF}$=$\frac{2\sqrt{2}}{2}$=$\sqrt{2}$.
∴$\frac{AB}{DE}$=$\frac{BC}{EF}$,
∴△ABC∽△DEF.
点评 此题考查的是相似三角形的判定,解答此题的关键是认真观察图形,得出两个三角形角和角,边和边的关系.

练习册系列答案
相关题目
17.已知菱形ABCD的对角线AC与BD交于点O,则下列结论正确的是( )
| A. | 点O到顶点A的距离大于到顶点B的距离 | |
| B. | 点O到顶点A的距离等于到顶点B的距离 | |
| C. | 点O到边AB的距离大于到边BC的距离 | |
| D. | 点O到边AB的距离等于到边BC的距离 |
 如图,已知一次函数y=-x+1的图象与x轴、y轴分别交于A点、B点,点M在坐标轴上,并且使以点A、B、M为顶点的三角形是等腰三角形,则这样的点M有7个.
如图,已知一次函数y=-x+1的图象与x轴、y轴分别交于A点、B点,点M在坐标轴上,并且使以点A、B、M为顶点的三角形是等腰三角形,则这样的点M有7个.
 如图是圆心角为30°,半径分别是1,3,5,7,…的扇形组成的图形,阴影部分的面积一次记为S1、S2、S3、…,则S11=14π(结果保留π).
如图是圆心角为30°,半径分别是1,3,5,7,…的扇形组成的图形,阴影部分的面积一次记为S1、S2、S3、…,则S11=14π(结果保留π). 如图,直线L1:y=bx+c与抛物线L2:y=ax2的两个交点坐标分别为A(m,4),B(1,1).
如图,直线L1:y=bx+c与抛物线L2:y=ax2的两个交点坐标分别为A(m,4),B(1,1).