题目内容
14.小明遇到这样一个问题:如图1,△ABC是等边三角形,点D为BC的中点,且满足∠ADE=60°,DE交等边△ABC外角平分线CE所在直线于点E,试探究AD与DE的数量关系.小明发现,过点D作DF∥AC,交AB于点F,通过构造全等三角形,经过推理论证,能够得到AD与DE的数量关系.(1)AD与DE相等吗?请你说明理由;
【类比探究】
(2)当点D是线段BC上(不与点B,C重合)任意一点时,其它条件不变,如图2,试猜想AD与DE之间的数量关系,并证明你的结论;
【拓展应用】
(3)当点D在BC的延长线上,且满足CD=BC,连接AE,其它条件不变,如图3,若AD=6,求DE的长.

分析 (1)结论:AD=DE.由等边三角形的性质和平行线的性质得到∠BDF=∠BFD=60°,于是得到△BDF是等边三角形,再证明△AFD≌△DCE即可得到结论;
(2)结论:AD=DE.由等边三角形的性质和平行线的性质得到∠BDF=∠BFD=60°,于是得到△BDF是等边三角形,再证明△AFD≌△DCE即可得到结论;
(3)由BC=CD,得到AC=CD,得到CE垂直平分AD,证出△ADE是等边三角形,即可解决问题.
解答 解:(1)结论:AD=DE,理由如下:
如图1中,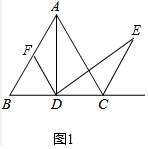
∵△ABC是等边三角形,
∴AB=BC,∠B=∠ACB=∠ABC=60°.
又∵DF∥AC,
∴∠BDF=∠BFD=60°,
∴△BDF是等边三角形,
∴DF=BD,∠BFD=60°,
∵BD=CD,
∴DF=CD
∴∠AFD=120°.
∵EC是外角的平分线,
∠DCE=120°=∠AFD,
∵∠ADB=∠ADC=90°,
∴∠ADF=∠ECD=30°,
在△AFD与△EDC中,
$\left\{\begin{array}{l}{∠AFD=∠DCE}\\{DF=CD}\\{∠ADF=∠EDC}\end{array}\right.$,
∴△AFD≌△DCE(ASA),
∴AD=DE;
(2)结论:AD=DE;理由如下:
如图2,过点D作DF∥AC,交AB于点F,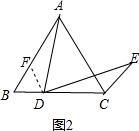
∵△ABC是等边三角形,
∴AB=BC,∠B=∠ACB=∠ABC=60°,
又∵DF∥AC,
∴∠BDF=∠BFD=60°,
∴△BDF是等边三角形,BF=BD,∠BFD=60°,
∴AF=CD,∠AFD=120°,
∵EC是外角的平分线,
∠DCE=120°=∠AFD,
∵∠ADC是△ABD的外角,
∴∠ADC=∠B+∠FAD=60°+∠FAD,
∵∠ADC=∠ADE+∠EDC=60°+∠EDC,
∴∠ADF=∠EDC,
在△AFD≌△DCE中,
$\left\{\begin{array}{l}{∠ADF=∠EDC}\\{AF=CD}\\{∠AFD=∠DCE}\end{array}\right.$,
∴△AFD≌△DCE(ASA),
∴AD=DE;
(3)如图3中,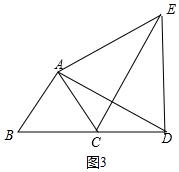
∵BC=CD,
∴AC=CD,
∵CE平分∠ACD,
∴CE垂直平分AD,
∴AE=DE,
∵∠ADE=60°,
∴△ADE是等边三角形,
∴DE=AD=6.
点评 本题主要考查了全等三角形的性质与判定,等边三角形的性质,平行线的性质,线段的垂直平分线的性质等知识,解题的关键是熟练掌握全等三角形的判定和性质,学会添加常用辅助线,构造全等三角形解决问题,属于中考压轴题.

 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案| A. | 七边形 | B. | 八边形 | C. | 九边形 | D. | 十边形 |
| A. | (x-4)(x+3) | B. | (x-6)(x+2) | C. | (x-4)(x-3) | D. | (x+6)(x-2) |
| A. | y随x的增大而增大 | |
| B. | 函数图象与坐标轴围成的三角形面积为18 | |
| C. | 函数图象不经过第四象限 | |
| D. | 函数图象与x轴正方向夹角为30° |
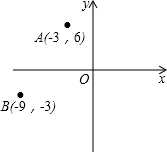 如图,在平面直角坐标系中,已知点A(-3,6),B(-9,-3),以原点O为位似中心,相似比为$\frac{1}{3}$,把△ABO缩小,则点A的对应点A′的坐标是(-1,2)或(1,-2).
如图,在平面直角坐标系中,已知点A(-3,6),B(-9,-3),以原点O为位似中心,相似比为$\frac{1}{3}$,把△ABO缩小,则点A的对应点A′的坐标是(-1,2)或(1,-2). 如图AD∥BC,∠A=30°,∠D=70°,作射线CE∥AB,则∠DCE=80°或100°.
如图AD∥BC,∠A=30°,∠D=70°,作射线CE∥AB,则∠DCE=80°或100°. 阳光下,小亮测量“望月阁”的高AB.(如图),由于观测点与“望月阁”底部间的距离不易测得,因此他首先在直线BM上点C处固定平放一平面镜,在镜面上做了一个标记,小亮看着镜面上的标记,他来回走动,走到点D时,看到“望月阁”顶端点A在镜面中的像与镜面上的标记重合,这时,测得小亮眼睛与地面的高度ED=1.5米,CD=2米.然后,在阳光下,他们用测影长的方法进行了第二次测量,方法如下:小亮从D点沿DM方向走了16米,到达“望月阁”影子的末端F点处,此时,测得小亮身高FG的影长FH=2.5米,FG=1.65米.已知AB⊥BM,ED⊥BM,GF⊥BM,其中,测量时所使用的平面镜的厚度忽略不计,请你根据题中提供的相关信息,求出“望月阁”的高AB的长度.
阳光下,小亮测量“望月阁”的高AB.(如图),由于观测点与“望月阁”底部间的距离不易测得,因此他首先在直线BM上点C处固定平放一平面镜,在镜面上做了一个标记,小亮看着镜面上的标记,他来回走动,走到点D时,看到“望月阁”顶端点A在镜面中的像与镜面上的标记重合,这时,测得小亮眼睛与地面的高度ED=1.5米,CD=2米.然后,在阳光下,他们用测影长的方法进行了第二次测量,方法如下:小亮从D点沿DM方向走了16米,到达“望月阁”影子的末端F点处,此时,测得小亮身高FG的影长FH=2.5米,FG=1.65米.已知AB⊥BM,ED⊥BM,GF⊥BM,其中,测量时所使用的平面镜的厚度忽略不计,请你根据题中提供的相关信息,求出“望月阁”的高AB的长度. 如图,在4×4的正方形方格中,△ABC和△DEF的顶点都在边长为1的小正方形的顶点上.
如图,在4×4的正方形方格中,△ABC和△DEF的顶点都在边长为1的小正方形的顶点上.