题目内容
6.若a、b为有理数,且$\sqrt{18}$+$\sqrt{9}$+$\sqrt{\frac{1}{8}}$=a+b$\sqrt{2}$,则$\frac{a}{b}$=$\frac{12}{13}$.分析 已知等式整理后,根据实数相等的条件求出a与b的值,即可确定出原式的值.
解答 解:已知等式整理得:3$\sqrt{2}$+3+$\frac{\sqrt{2}}{4}$=3+$\frac{13}{4}$$\sqrt{2}$=a+b$\sqrt{2}$,
∴a=3,b=$\frac{13}{4}$,
则原式=$\frac{12}{13}$.
故答案为:$\frac{12}{13}$.
点评 此题考查了实数的运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
16.已知a+b=5,ab=4,则ab2+a2b-a-b的值是( )
| A. | -15 | B. | 15 | C. | 6 | D. | -6 |
15. 如图,射线BA、CA交于点A.连接BC,已知∠B=∠C=40°,那么∠α=( )度.
如图,射线BA、CA交于点A.连接BC,已知∠B=∠C=40°,那么∠α=( )度.
 如图,射线BA、CA交于点A.连接BC,已知∠B=∠C=40°,那么∠α=( )度.
如图,射线BA、CA交于点A.连接BC,已知∠B=∠C=40°,那么∠α=( )度.| A. | 60 | B. | 70 | C. | 80 | D. | 90 |
16.柯南的妈妈是一个炒股迷,上周又到股市去买了股票,根据他们的对话(如图)解决问题.

(1)星期二收盘时,每股是多少元?
(2)本周内最高价是每股多少元,最低价是每股多少元?
| 星期 | 一 | 二 | 三 | 四 | 五 |
| 每股涨跌 | +4 | +4.5 | -1 | -2.5 | -6 |

(1)星期二收盘时,每股是多少元?
(2)本周内最高价是每股多少元,最低价是每股多少元?
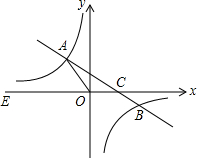 如图,在平面直角坐标系xOy中,一次函数的图象y=kx+b(k≠0)与反比例函数y=$\frac{m}{x}$(m≠0)的图象交于二、四象限内的A、B两点,与x轴交于C点,线段OA=5,OC=3,E为x轴上一点,且tan∠AOE=$\frac{4}{3}$.
如图,在平面直角坐标系xOy中,一次函数的图象y=kx+b(k≠0)与反比例函数y=$\frac{m}{x}$(m≠0)的图象交于二、四象限内的A、B两点,与x轴交于C点,线段OA=5,OC=3,E为x轴上一点,且tan∠AOE=$\frac{4}{3}$. 某校有一块四边形草地如图所示,已经测量出它的四条边长AB=6m,AD=8m,BC=26m,CD=24m,且∠A=90°
某校有一块四边形草地如图所示,已经测量出它的四条边长AB=6m,AD=8m,BC=26m,CD=24m,且∠A=90°