题目内容
15.问题背景:如图(1),在△ABC中,已知AB=AC,BE=CF.(1)发现问题:小华审题后发现,若连接CE,BF,则CE=BF,请说明理由;
(2)提出问题:如图(2),设CE与BF交于点O,则直线AO是BC边的垂直平分线吗?试说明理由;
(3)解决问题:在图(3)中,是各边相等,各内角也相等的正五边形ABCDE,请你只用无刻度的直尺画出图中BC边的垂直平分线.

分析 (1)证明△EBC≌△FCB即可;
(2)证明△EOB≌△FOC,得到OB=OC,根据线段垂直平分线的判定定理得到答案;
(3)根据点到线段的两个端点的距离相等的点在线段的垂直平分线上作图即可.
解答 解:(1)如图1中,连接EC、BF.
∵AB=AC,
∴∠ABC=∠ACB,
在△EBC和△FCB中,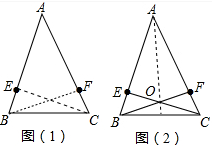
$\left\{\begin{array}{l}{BE=CF}\\{∠ABC=∠ACB}\\{BC=CB}\end{array}\right.$,
∴△EBC≌△FCB,
∴CE=BF;
(2)结论:AO是BC边的中垂线,
理由:∵△EBC≌△FCB,
∴∠OEB=∠OFC,
在△EOB和△FOC中,
$\left\{\begin{array}{l}{∠OEB=∠OFC}\\{∠EOB=∠FOC}\\{BE=CF}\end{array}\right.$,
∴△EOB≌△FOC,
∴OB=OC,又AB=AC,
∴AO是BC边的中垂线;
(3)如图(3):连接AC、BD交于点O,作直线EO,直线EO即为线段BC的垂直平分线.
点评 本题考查的是线段垂直平分线的性质、等腰三角形的性质,掌握线段的垂直平分线上的点到线段的两个端点的距离相等是解题的关键.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
10. 如图,在方格纸中,△ABC经过变换得到△DEF,正确的变换是( )
如图,在方格纸中,△ABC经过变换得到△DEF,正确的变换是( )
 如图,在方格纸中,△ABC经过变换得到△DEF,正确的变换是( )
如图,在方格纸中,△ABC经过变换得到△DEF,正确的变换是( )| A. | 把△ABC向下平移4格,再绕点C逆时针方向旋转180° | |
| B. | 把△ABC向下平移5格,再绕点C顺时针方向旋转180° | |
| C. | 把△ABC绕点C逆时针方向旋转90°,再向下平移2格 | |
| D. | 把△ABC绕点C顺时针方向旋转90°,再向下平移5格 |
5.公交公司的某路公交车每月运营总支出的费用为4000元,乘客乘车的票价为2元/人次.设每月的乘客量为x(人次),每月的赢利额为y(元).(赢利额=总收入-总支出)
(1)y(元)与x(人次)之间的关系式为y=2x-4000;(x为正整数)
(2)根据关系式填表:
(3)根据表格数据,当月乘客量超过2000人次时,该路公交车运营才能赢利.
(1)y(元)与x(人次)之间的关系式为y=2x-4000;(x为正整数)
(2)根据关系式填表:
| x/人次 | 500 | 1000 | 1500 | 2000 | 2500 | 3000 |
| y/元 | -3000 | -2000 | -1000 | 0 | 1000 | 2000 |

 如图,AB∥CD,则∠1+∠3-∠2的度数等于180°.
如图,AB∥CD,则∠1+∠3-∠2的度数等于180°. 如图,已知平行四边形ABCD,延长AD到E,使DE=AD,连接BE与DC交于O点.
如图,已知平行四边形ABCD,延长AD到E,使DE=AD,连接BE与DC交于O点.