题目内容
6.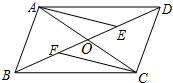 如图,已知四边形ABCD的对角线AC、BD相交于点O,OB=OD,BF=DE,AE∥CF.
如图,已知四边形ABCD的对角线AC、BD相交于点O,OB=OD,BF=DE,AE∥CF.(1)求证:△OAE≌△OCF;
(2)若OA=OD,猜想:四边形ABCD的形状,请证明你的结论.
分析 (1)由AE∥CF,得到两对内错角相等,再由OB=OD,BF=DE,得到OE=OF,利用AAS即可得证;
(2)若OA=OD,则四边形ABCD为矩形,理由为:由OA=OD,得到OB=OC,即OD=OA=OC=OB,利用对角线互相平分且相等的四边形为矩形即可得证.
解答 (1)证明:∵AE∥CF,
∴∠AEO=∠CFO,∠EAO=∠FCO,
∵OB=OD,BF=DE,
∴OB-BF=OD-DE,
即OE=OF,
在△OAE和△OCF中,
$\left\{\begin{array}{l}{∠AEO=∠CFO}\\{∠EAO=∠FCO}\\{OE=OF}\end{array}\right.$,
∴△OAE≌△OCF(AAS);
(2)若OA=OD,则四边形ABCD是矩形,理由为:
证明:∵△OAE≌△OCF,
∴OA=OC,
∵OD=OA,
∴OA=OB=OC=OD,且BD=AC,
∴四边形ABCD为矩形.
点评 此题考查了全等三角形的判定与性质,矩形的判定与性质,以及平行线的性质,熟练掌握全等三角形的判定与性质是解本题的关键.

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案
相关题目
17.在?ABCD中,对角线AC、BD相交于点O,若AC=8,BD=6,AB=5,则△AOB的周长为( )
| A. | 11 | B. | 12 | C. | 13 | D. | 14 |
14.已知等腰三角形的两条边长分别是5cm、11cm,则该三角形的周长是( )
| A. | 16cm | B. | 21cm | C. | 27cm | D. | 21cm或27cm |
11. 如图,将矩形纸片ABCD沿CE向上折叠,使点B落在AD边上的点F处,若AE=$\frac{1}{2}$BE,则$\frac{CD}{BC}$=( )
如图,将矩形纸片ABCD沿CE向上折叠,使点B落在AD边上的点F处,若AE=$\frac{1}{2}$BE,则$\frac{CD}{BC}$=( )
 如图,将矩形纸片ABCD沿CE向上折叠,使点B落在AD边上的点F处,若AE=$\frac{1}{2}$BE,则$\frac{CD}{BC}$=( )
如图,将矩形纸片ABCD沿CE向上折叠,使点B落在AD边上的点F处,若AE=$\frac{1}{2}$BE,则$\frac{CD}{BC}$=( )| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | $\frac{3}{2}$ | D. | 2 |
15. 如图,在等腰直角△ABC中,∠C=90°,AD是∠CAB的平分线,DE⊥AB,且DE=2cm,则AE的长是( )cm.
如图,在等腰直角△ABC中,∠C=90°,AD是∠CAB的平分线,DE⊥AB,且DE=2cm,则AE的长是( )cm.
 如图,在等腰直角△ABC中,∠C=90°,AD是∠CAB的平分线,DE⊥AB,且DE=2cm,则AE的长是( )cm.
如图,在等腰直角△ABC中,∠C=90°,AD是∠CAB的平分线,DE⊥AB,且DE=2cm,则AE的长是( )cm.| A. | 2$\sqrt{2}$+2 | B. | 2$\sqrt{3}$ | C. | 4 | D. | 不确定 |
 如图,△ABC的顶点都在方格纸的格点上.
如图,△ABC的顶点都在方格纸的格点上.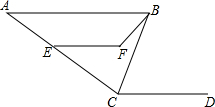 如图,AB∥CD,CB平分∠ACD,∠ACD=140°,∠CBF=20°,∠EFB=130°.求∠CEF的度数.
如图,AB∥CD,CB平分∠ACD,∠ACD=140°,∠CBF=20°,∠EFB=130°.求∠CEF的度数.