题目内容
17.在?ABCD中,对角线AC、BD相交于点O,若AC=8,BD=6,AB=5,则△AOB的周长为( )| A. | 11 | B. | 12 | C. | 13 | D. | 14 |
分析 根据平行四边形对角线互相平分,求出OA、OB即可解决问题.
解答 解:如图,∵四边形ABCD是平行四边形,
∴AO=OC=$\frac{1}{2}$AC=4,BO=OD=$\frac{1}{2}$BD=3,
∵AB=5,
∴△AOB的周长为OA+OB+AB=4+3+5=12.
故选B.
点评 本题考查平行四边形的性质,三角形周长等知识,解题的关键是记住平行四边形的性质:对角线互相平分,属于中考基础题,常考题型.

练习册系列答案
相关题目
8.已知关于x、y的方程组$\left\{\begin{array}{l}{4x+3y=1}\\{x-3y=m}\end{array}\right.$的解互为相反数,则m的值为( )
| A. | -$\frac{7}{4}$ | B. | $\frac{1}{2}$ | C. | -4 | D. | 4 |
12. 如图,?ABCD中,∠B=70°,DE是角平分线,则∠CDE=( )
如图,?ABCD中,∠B=70°,DE是角平分线,则∠CDE=( )
 如图,?ABCD中,∠B=70°,DE是角平分线,则∠CDE=( )
如图,?ABCD中,∠B=70°,DE是角平分线,则∠CDE=( )| A. | 110° | B. | 70° | C. | 35° | D. | 55° |
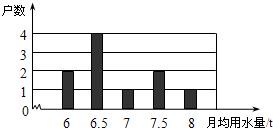 我国是世界上严重缺失的国家之一,为了倡导“节约用水从我做起”,小刚在他所在班的50名同学中,随机调查了10名同学家庭中一年的月均用水量(单位:t),并将调查结果绘成了如图的条形统计图,则这10个样本数据的中位数是6.5t.
我国是世界上严重缺失的国家之一,为了倡导“节约用水从我做起”,小刚在他所在班的50名同学中,随机调查了10名同学家庭中一年的月均用水量(单位:t),并将调查结果绘成了如图的条形统计图,则这10个样本数据的中位数是6.5t.



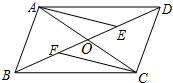 如图,已知四边形ABCD的对角线AC、BD相交于点O,OB=OD,BF=DE,AE∥CF.
如图,已知四边形ABCD的对角线AC、BD相交于点O,OB=OD,BF=DE,AE∥CF.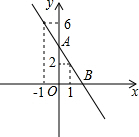 如图,一次函数y=ax+b的图象经过点(1,2),点(-1,6),且与x轴交于点B,与y轴交于点A.
如图,一次函数y=ax+b的图象经过点(1,2),点(-1,6),且与x轴交于点B,与y轴交于点A.