题目内容
11. 如图,将矩形纸片ABCD沿CE向上折叠,使点B落在AD边上的点F处,若AE=$\frac{1}{2}$BE,则$\frac{CD}{BC}$=( )
如图,将矩形纸片ABCD沿CE向上折叠,使点B落在AD边上的点F处,若AE=$\frac{1}{2}$BE,则$\frac{CD}{BC}$=( )| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | $\frac{3}{2}$ | D. | 2 |
分析 根据矩形的性质可得∴∠A=∠D=∠B=90°,由折叠可得FC=BC,EB=EF,∠B=∠EFC=90°,然后利用特殊角的三角函数可求出∠AFE的度数,进而可得∠DFC的度数,再利用三角函数可得$\frac{CD}{FC}$,进而可得$\frac{CD}{BC}$.
解答 解:∵四边形ABCD是矩形,
∴∠A=∠D=∠B=90°,
由折叠可得FC=BC,EB=EF,∠B=∠EFC=90°,
∵AE=$\frac{1}{2}$BE,
∴$\frac{AE}{EF}$=$\frac{1}{2}$,
∴∠AFE=30°,
∴∠DFC=60°,
∵sin60°=$\frac{DC}{FC}$=$\frac{\sqrt{3}}{2}$,
∴$\frac{CD}{BC}$=$\frac{\sqrt{3}}{2}$,
故选:B.
点评 此题主要考查了矩形的性质,以及图形的翻折变换和三角函数,关键是找准折叠后哪些角和边是对应相等的.

练习册系列答案
 阶梯计算系列答案
阶梯计算系列答案
相关题目
19.若一个多边形每一个内角都是135°,则这个多边形的边数为( )
| A. | 9 | B. | 8 | C. | 6 | D. | 5 |
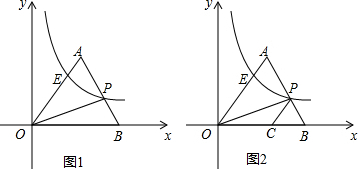




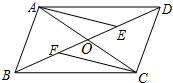 如图,已知四边形ABCD的对角线AC、BD相交于点O,OB=OD,BF=DE,AE∥CF.
如图,已知四边形ABCD的对角线AC、BD相交于点O,OB=OD,BF=DE,AE∥CF.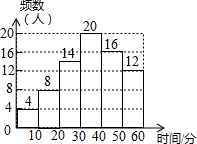 小文同学统计了他所在小区居民每天微信阅读的时间,并绘制了直方图.
小文同学统计了他所在小区居民每天微信阅读的时间,并绘制了直方图.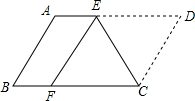 如图,将?ABCD沿CE折叠,使点D落在BC边上的F处,点E在AD上.
如图,将?ABCD沿CE折叠,使点D落在BC边上的F处,点E在AD上.