题目内容
18.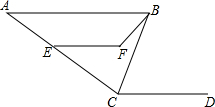 如图,AB∥CD,CB平分∠ACD,∠ACD=140°,∠CBF=20°,∠EFB=130°.求∠CEF的度数.
如图,AB∥CD,CB平分∠ACD,∠ACD=140°,∠CBF=20°,∠EFB=130°.求∠CEF的度数.
分析 由CB平分∠ACD,∠ACD=140°,推出∠DCB=70°,由AB∥CD,证得∠CBA=∠DCB=70°,进而求得∠FAB,故得到∠EFB+∠FBA=180°,由平行线的判定证得EF∥AB,即可证得∠CEF=∠A,从而求出∠ACD=140°,即可证得结论.
解答 解:∵CB平分∠ACD,∠ACD=140°,
∴∠DCB=70°,
∵AB∥CD,
∴∠CBA=∠DCB=70°,
∵∠CBF=20°,
∴∠FAB=70°-20°=50°,
∵∠EFB=130°,
∴∠EFB+∠FBA=180°,
∴EF∥AB,
∴∠CEF=∠A,
∵AB∥CD,∠ACD=140°,
∴∠A=180-140°=40°,
∴∠CEF=40°.
点评 此题主要考查了平行线的判定与性质,角的平分线的性质,根据已知得出AB∥EF是解题关键.

练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目
8.已知关于x、y的方程组$\left\{\begin{array}{l}{4x+3y=1}\\{x-3y=m}\end{array}\right.$的解互为相反数,则m的值为( )
| A. | -$\frac{7}{4}$ | B. | $\frac{1}{2}$ | C. | -4 | D. | 4 |
13.在平面直角坐标平面内,点P到x轴的距离是5,到y轴的距离是3,并且点P在第四象限,则点P的坐标是( )
| A. | (3,-5) | B. | (5,-3) | C. | (-3,5) | D. | (-3,5)或(3,-5) |
10.据外汇局网站5月16日消息:国家外汇管理局统计数据显示,2016年4月,银行结售汇逆差1534亿元人民币,其中“1534亿”用科学记数法表示为( )
| A. | 1.534×103 | B. | 1.534×1011 | C. | 15.34×108 | D. | 1534×108 |
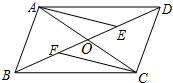 如图,已知四边形ABCD的对角线AC、BD相交于点O,OB=OD,BF=DE,AE∥CF.
如图,已知四边形ABCD的对角线AC、BD相交于点O,OB=OD,BF=DE,AE∥CF.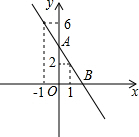 如图,一次函数y=ax+b的图象经过点(1,2),点(-1,6),且与x轴交于点B,与y轴交于点A.
如图,一次函数y=ax+b的图象经过点(1,2),点(-1,6),且与x轴交于点B,与y轴交于点A.