题目内容
2.己知反比例函数:y=$\frac{{k}_{1}}{x}$与一次函数y=k2x+b的图象交于点A(1,8)、B(-4,m).(1)分别求反比例函数和一次函数的解析式;
(2)若M(x1,y1)、N(x2,y2)是反比例函数y=$\frac{{k}_{1}}{x}$图象上的两点,且x1<x2,y1<y2,指出点M,N各位于哪个象限,并简要说明理由.
分析 (1)由点A的坐标结合反比例函数图象上点的坐标特征即可求出反比例函数的解析式;再利用反比例函数图象上点的坐标特征求出点B的坐标,再由A、B的坐标利用待定系数法即可求出一次函数解析式;
(2)由k1的值结合反比例函数的性质即可分析出点M、N所在的象限.
解答 解:(1)∵反比例函数y=$\frac{{k}_{1}}{x}$与一次函数y=k2x+b的图象交于点A(1,8)、B(-4,m),
∴k1=1×8=8,
∴反比例函数的解析式为y=$\frac{8}{x}$.
∵-4m=8,解得:m=-2,
∴点B的坐标为(-4,-2).
把A(1,8)、B(-4,-2)代入一次函数y=k2x+b中,
∴$\left\{\begin{array}{l}{8={k}_{2}+b}\\{-2=-4{k}_{2}+b}\end{array}\right.$,
∴解得:$\left\{\begin{array}{l}{{k}_{2}=2}\\{b=6}\end{array}\right.$,
∴一次函数的解析式为y=2x+6.
(2)∵反比例函数y=$\frac{8}{x}$的图象位于一、三象限,
∴在每个象限内,y随x的增大而减小,
∵x1<x2,y1<y2,
∴M,N在不同的象限,)
∴M(x1,y1)在第三象限,N(x2,y2)在第一象限.
点评 本题考查了反比例函数与一次函数的交点问题、待定系数法求函数解析式、反比例函数图象上点的坐标特征以及反比例函数的性质,解题的关键是:(1)求出点B的坐标;(2)根据反比例函数的性质确定其在每个象限内的单调性.本题属于基础题,难度不大,解决该题型题目时,先求出来点的坐标,再由点的坐标利用待定系数法求出函数解析式是关键.

练习册系列答案
相关题目
4.下列计算正确的是( )
| A. | $\sqrt{2}$×$\sqrt{5}$=$\sqrt{10}$ | B. | x8÷x2=x4 | C. | (2a)3=6a3 | D. | 3a5•2a3=6a6 |
10. 如图,已知DE为三角形ABC的中位线,且AB=8,AC=7,BC=6,则三角形ADE的周长( )
如图,已知DE为三角形ABC的中位线,且AB=8,AC=7,BC=6,则三角形ADE的周长( )
 如图,已知DE为三角形ABC的中位线,且AB=8,AC=7,BC=6,则三角形ADE的周长( )
如图,已知DE为三角形ABC的中位线,且AB=8,AC=7,BC=6,则三角形ADE的周长( )| A. | 21 | B. | 10.5 | C. | 18 | D. | 17 |
11.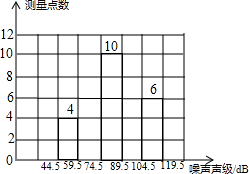 为了增强环境保护意识,在“世界环境日”当天,在环保局工作人员指导下,若干名“环保小卫士”组成的“控制噪声污染”课题学习研究小组,随机抽查了全市40个噪声测量点在某时刻的噪声声级(单位:dB),并将抽查得到的数据进行整理(设所测数据是正整数),得频数分布表如表:
为了增强环境保护意识,在“世界环境日”当天,在环保局工作人员指导下,若干名“环保小卫士”组成的“控制噪声污染”课题学习研究小组,随机抽查了全市40个噪声测量点在某时刻的噪声声级(单位:dB),并将抽查得到的数据进行整理(设所测数据是正整数),得频数分布表如表:
根据表中提供的信息解答下列问题:
(1)频数分布表中的a=8,b=12,c=0.3;
(2)补充完整频数分布直方图;
(3)如果全市共有400个测量点,那么在这一时刻噪声声级小于75dB的测量点约有多少个?
 为了增强环境保护意识,在“世界环境日”当天,在环保局工作人员指导下,若干名“环保小卫士”组成的“控制噪声污染”课题学习研究小组,随机抽查了全市40个噪声测量点在某时刻的噪声声级(单位:dB),并将抽查得到的数据进行整理(设所测数据是正整数),得频数分布表如表:
为了增强环境保护意识,在“世界环境日”当天,在环保局工作人员指导下,若干名“环保小卫士”组成的“控制噪声污染”课题学习研究小组,随机抽查了全市40个噪声测量点在某时刻的噪声声级(单位:dB),并将抽查得到的数据进行整理(设所测数据是正整数),得频数分布表如表:| 组 别 | 噪声声级分组 | 频 数 | 频 率 |
| 1 | 44.5-59.5 | 4 | 0.1 |
| 2 | 59.5-74.5 | a | 0.2 |
| 3 | 74.5-89.5 | 10 | 0.25 |
| 4 | 89.5-104.5 | b | c |
| 5 | 104.5-119.5 | 6 | 0.15 |
| 合 计 | 40 | 1.00 |
(1)频数分布表中的a=8,b=12,c=0.3;
(2)补充完整频数分布直方图;
(3)如果全市共有400个测量点,那么在这一时刻噪声声级小于75dB的测量点约有多少个?
 如图,在平行四边形ABCD中,AB=3,AD=4,∠ABC=60°,过BC的中点E作EF⊥AB于点F,交DC的延长线于点G,则DE=$\sqrt{19}$.
如图,在平行四边形ABCD中,AB=3,AD=4,∠ABC=60°,过BC的中点E作EF⊥AB于点F,交DC的延长线于点G,则DE=$\sqrt{19}$.