题目内容
17.已知⊙O1与⊙O2相交于A、B两点,连心线O1O2交AB于点C,O1A=$3\sqrt{2}$,O2A=$2\sqrt{3}$,AB=6.求∠O1AO2的度数.分析 分两种情形:①如图1中,当点C在线段O1O2上时,根据∠O1AO2=∠O1AC+∠O2AC即可解决问题,②如图2中,当点C在O1O2的延长线上时,根据∠O1AO2=∠O1AC-∠O2AC即可解决问题.
解答 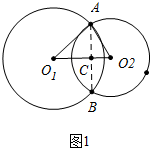 解:如图1中,当点C在线段O1O2上时,
解:如图1中,当点C在线段O1O2上时,
∵AB⊥O1O2,AC=BC=3,
∴∠ACO2=∠ACO1=90°,
∵AO2=2$\sqrt{3}$,
∴CO2=$\sqrt{A{{O}_{2}}^{2}-A{C}^{2}}$=$\sqrt{3}$,
∴AO2=2CO2,
∴∠CAO2=30°,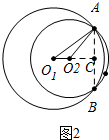 ∵AO1=3$\sqrt{2}$,AC=3,
∵AO1=3$\sqrt{2}$,AC=3,
∴CO1=$\sqrt{A{{O}_{1}}^{2}-A{C}^{2}}$=3,
∴AC=CO1,
∴∠CAO1=45°,
∴∠O1AO2=∠O1AC+∠O2AC=45°+30°=75°,
如图2中,当点C在O1O2的延长线上时,
∠O1AO2=∠O1AC-∠O2AC=45°-30°=15°.
∴∠O1AO2的度数为75°或15°.
点评 本题考查相交两个圆的性质、直角三角形30度角的判定等腰直角三角形的判定等知识,解题的关键是正确画出图形,注意有两个解,属于中考常考题型.

练习册系列答案
相关题目
 二次函数y=ax2+bx+c的图象经过点(-1,4),且与直线y=-$\frac{1}{2}$x+1相交于A、B两点(如图),A点在y轴上,过点B作BC⊥x轴,垂足为点C(-3,0).
二次函数y=ax2+bx+c的图象经过点(-1,4),且与直线y=-$\frac{1}{2}$x+1相交于A、B两点(如图),A点在y轴上,过点B作BC⊥x轴,垂足为点C(-3,0). 如图,OD是⊙O的半径,弦AB⊥OD于E,若∠O=70°,则∠A+∠C=55度.
如图,OD是⊙O的半径,弦AB⊥OD于E,若∠O=70°,则∠A+∠C=55度.
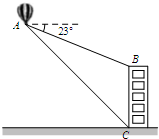 如图,在热气球上A处测得一栋大楼顶部B的俯角为23°,测得这栋大楼底部C的俯角为45°.已知热气球A处距地面的高度为180m,求这栋大楼的高度(精确到1m).参考数据:sin23°=0.39,cos23°=0.92,tan23°=0.42.
如图,在热气球上A处测得一栋大楼顶部B的俯角为23°,测得这栋大楼底部C的俯角为45°.已知热气球A处距地面的高度为180m,求这栋大楼的高度(精确到1m).参考数据:sin23°=0.39,cos23°=0.92,tan23°=0.42.