题目内容
7. 如图,在平行四边形ABCD中,AB=3,AD=4,∠ABC=60°,过BC的中点E作EF⊥AB于点F,交DC的延长线于点G,则DE=$\sqrt{19}$.
如图,在平行四边形ABCD中,AB=3,AD=4,∠ABC=60°,过BC的中点E作EF⊥AB于点F,交DC的延长线于点G,则DE=$\sqrt{19}$.
分析 由平行四边形的性质得出CD=AB=3,BC=AD=4,AB∥CD,由平行线的性质得出∠GCE=∠B=60°,证出EF⊥DG,由含30°角的直角三角形的性质得出CG=$\frac{1}{2}$CE=1,求出EG=$\sqrt{3}$CG=$\sqrt{3}$,DG=CD+CG=4,由勾股定理求出DE即可.
解答 解:∵四边形ABCD是平行四边形,
∴CD=AB=3,BC=AD=4,AB∥CD,
∴∠GCE=∠B=60°,
∵E是BC的中点,
∴CE=BE=2,
∵EF⊥AB,
∴EF⊥DG,
∴∠G=90°,
∴CG=$\frac{1}{2}$CE=1,
∴EG=$\sqrt{3}$CG=$\sqrt{3}$,DG=CD+CG=3+1=4,
∴DE=$\sqrt{E{G}^{2}+D{G}^{2}}$=$\sqrt{(\sqrt{3})^{2}+{4}^{2}}$=$\sqrt{19}$;
故答案为:$\sqrt{19}$.
点评 本题考查了平行四边形的性质、含30°角的直角三角形的性质、勾股定理;熟练掌握平行四边形的性质,由含30°角的直角三角形的性质求出CG是解决问题的关键.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
12. 如图,在空白网格内将某一个小正方形涂成阴影部分,且所涂的小正方形与原阴影图形的小正方形至少有一边重合.小红按要求涂了一个正方形,所得到的阴影图形恰好是轴对称图形的概率为( )
如图,在空白网格内将某一个小正方形涂成阴影部分,且所涂的小正方形与原阴影图形的小正方形至少有一边重合.小红按要求涂了一个正方形,所得到的阴影图形恰好是轴对称图形的概率为( )
 如图,在空白网格内将某一个小正方形涂成阴影部分,且所涂的小正方形与原阴影图形的小正方形至少有一边重合.小红按要求涂了一个正方形,所得到的阴影图形恰好是轴对称图形的概率为( )
如图,在空白网格内将某一个小正方形涂成阴影部分,且所涂的小正方形与原阴影图形的小正方形至少有一边重合.小红按要求涂了一个正方形,所得到的阴影图形恰好是轴对称图形的概率为( )| A. | $\frac{1}{5}$ | B. | $\frac{4}{15}$ | C. | $\frac{4}{9}$ | D. | $\frac{1}{3}$ |
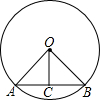 如图,在⊙O中,弦AB=6,圆心O到AB的距离OC=2,则⊙O的半径长为$\sqrt{13}$.
如图,在⊙O中,弦AB=6,圆心O到AB的距离OC=2,则⊙O的半径长为$\sqrt{13}$.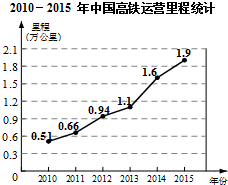 我国2010-2015年高铁运营里程情况统计如图所示,根据统计图提供的信息,预估2016年我国高铁运营里程约为2.2万公里,你的预估理由是每年平均增长量近似相等.
我国2010-2015年高铁运营里程情况统计如图所示,根据统计图提供的信息,预估2016年我国高铁运营里程约为2.2万公里,你的预估理由是每年平均增长量近似相等.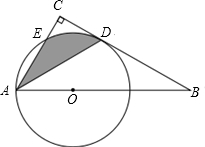 如图,Rt△ABC中,∠BAC=60°,点O为Rt△ABC斜边AB上的一点,以OA为半径的⊙O与BC切于点D,与AC交于点E,连接AD.
如图,Rt△ABC中,∠BAC=60°,点O为Rt△ABC斜边AB上的一点,以OA为半径的⊙O与BC切于点D,与AC交于点E,连接AD.