题目内容
5.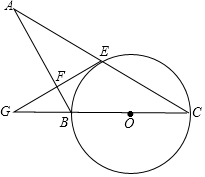 如图,在△ABC中,以BC为直径的⊙O交AC于点E,过点E作EF⊥AB于点F,延长EF交CB的延长线于点G,且∠ABG=2∠C.
如图,在△ABC中,以BC为直径的⊙O交AC于点E,过点E作EF⊥AB于点F,延长EF交CB的延长线于点G,且∠ABG=2∠C.(1)求证:EF是⊙O的切线;
(2)若sin∠EGC=$\frac{3}{5}$,⊙O的半径是3,求AF的长.
分析 (1)连接EO,由∠EOG=2∠C、∠ABG=2∠C知∠EOG=∠ABG,从而得AB∥EO,根据EF⊥AB得EF⊥OE,即可得证;
(2)由∠ABG=2∠C、∠ABG=∠C+∠A知∠A=∠C,即BA=BC=6,在Rt△OEG中求得OG=$\frac{OE}{sin∠EGO}$=5、BG=OG-OB=2,在Rt△FGB中求得BF=BGsin∠EGO,根据AF=AB-BF可得答案.
解答 解:(1)如图,连接EO,则OE=OC,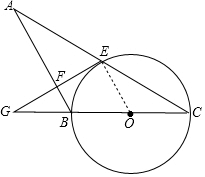
∴∠EOG=2∠C,
∵∠ABG=2∠C,
∴∠EOG=∠ABG,
∴AB∥EO,
∵EF⊥AB,
∴EF⊥OE,
又∵OE是⊙O的半径,
∴EF是⊙O的切线;
(2)∵∠ABG=2∠C,∠ABG=∠C+∠A,
∴∠A=∠C,
∴BA=BC=6,
在Rt△OEG中,∵sin∠EGO=$\frac{OE}{OG}$,
∴OG=$\frac{OE}{sin∠EGO}$=$\frac{3}{\frac{3}{5}}$=5,
∴BG=OG-OB=2,
在Rt△FGB中,∵sin∠EGO=$\frac{BF}{BG}$,
∴BF=BGsin∠EGO=2×$\frac{3}{5}$=$\frac{6}{5}$,
则AF=AB-BF=6-$\frac{6}{5}$=$\frac{24}{5}$.
点评 本题主要考查切线的判定与性质及解直角三角形的应用,熟练掌握切线的判定与性质及三角函数的定义是解题的关键.

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目
16. 如图,在正方形ABCD中,点E,F分别在BC,CD上,且∠EAF=45°,将△ABE绕点A顺时针旋转90°,使点E落在点E'处,则下列判断不正确的是( )
如图,在正方形ABCD中,点E,F分别在BC,CD上,且∠EAF=45°,将△ABE绕点A顺时针旋转90°,使点E落在点E'处,则下列判断不正确的是( )
 如图,在正方形ABCD中,点E,F分别在BC,CD上,且∠EAF=45°,将△ABE绕点A顺时针旋转90°,使点E落在点E'处,则下列判断不正确的是( )
如图,在正方形ABCD中,点E,F分别在BC,CD上,且∠EAF=45°,将△ABE绕点A顺时针旋转90°,使点E落在点E'处,则下列判断不正确的是( )| A. | △AEE′是等腰直角三角形 | B. | AF垂直平分EE' | ||
| C. | △E′EC∽△AFD | D. | △AE′F是等腰三角形 |
20. 如图所示的几何体的左视图( )
如图所示的几何体的左视图( )
 如图所示的几何体的左视图( )
如图所示的几何体的左视图( )| A. |  | B. |  | C. |  | D. |  |
17.下列计算正确的是( )
| A. | 20a+17c=37ac | B. | (x2y)3=x5y3 | ||
| C. | x3÷x6=x3 | D. | (a+b-1)2=a2+b2+1+2ab-2a-2b |
14. 如图,将△ABC平移后得到△DEF,若∠A=44°,∠EGC=70°,则∠ACB的度数是( )
如图,将△ABC平移后得到△DEF,若∠A=44°,∠EGC=70°,则∠ACB的度数是( )
 如图,将△ABC平移后得到△DEF,若∠A=44°,∠EGC=70°,则∠ACB的度数是( )
如图,将△ABC平移后得到△DEF,若∠A=44°,∠EGC=70°,则∠ACB的度数是( )| A. | 26° | B. | 44° | C. | 46° | D. | 66° |
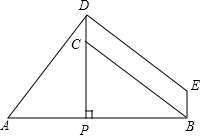 如图,点P在线段AB上,PD⊥AB,点C在线段PD上,连结BC,以CB,CD为邻边构造□BCDE,若AD=DE,AP=PC.
如图,点P在线段AB上,PD⊥AB,点C在线段PD上,连结BC,以CB,CD为邻边构造□BCDE,若AD=DE,AP=PC.