题目内容
16. 如图,在正方形ABCD中,点E,F分别在BC,CD上,且∠EAF=45°,将△ABE绕点A顺时针旋转90°,使点E落在点E'处,则下列判断不正确的是( )
如图,在正方形ABCD中,点E,F分别在BC,CD上,且∠EAF=45°,将△ABE绕点A顺时针旋转90°,使点E落在点E'处,则下列判断不正确的是( )| A. | △AEE′是等腰直角三角形 | B. | AF垂直平分EE' | ||
| C. | △E′EC∽△AFD | D. | △AE′F是等腰三角形 |
分析 由旋转的性质得到AE′=AE,∠E′AE=90°,于是得到△AEE′是等腰直角三角形,故A正确;由旋转的性质得到∠E′AD=∠BAE,由正方形的性质得到∠DAB=90°,推出∠E′AF=∠EAF,于是得到AF垂直平分EE',故B正确;根据余角的性质得到∠FE′E=∠DAF,于是得到△E′EC∽△AFD,故C正确;由于AD⊥E′F,但∠E′AD不一定等于∠DAE′,于是得到△AE′F不一定是等腰三角形,故D错误.
解答 解:∵将△ABE绕点A顺时针旋转90°,使点E落在点E'处,
∴AE′=AE,∠E′AE=90°,
∴△AEE′是等腰直角三角形,故A正确;
∵将△ABE绕点A顺时针旋转90°,使点E落在点E'处,
∴∠E′AD=∠BAE,
∵四边形ABCD是正方形,
∴∠DAB=90°,
∵∠EAF=45°,
∴∠BAE+∠DAF=45°,
∴∠E′AD+∠FAD=45°,
∴∠E′AF=∠EAF,
∵AE′=AE,
∴AF垂直平分EE',故B正确;
∵AF⊥E′E,∠ADF=90°,
∴∠FE′E+∠AFD=∠AFD+∠DAF,
∴∠FE′E=∠DAF,
∴△E′EC∽△AFD,故C正确;
∵AD⊥E′F,但∠E′AD不一定等于∠DAE′,
∴△AE′F不一定是等腰三角形,故D错误;
故选D.
点评 本题考查了旋转的性质,正方形的性质,相似三角形的判定,等腰直角三角形的判定,线段垂直平分线的判定,正确的识别图形是解题的关键.

练习册系列答案
 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
6.下表记录了甲、乙、丙、丁四名跳高运动员最近几次选拔赛成绩的平均数与方差:
根据表中数据,要从中选择一名成绩好且发挥稳定的运动员参加比赛,应该选择( )
| 甲 | 乙 | 丙 | 丁 | |
| 平均数(cm) | 180 | 185 | 185 | 180 |
| 方差 | 3.6 | 3.6 | 7.4 | 8.1 |
| A. | 甲 | B. | 乙 | C. | 丙 | D. | 丁 |
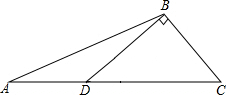 如图,在钝角△ABC中,过钝角顶点B作BD⊥BC交AC于点D.请用尺规作图法在BC边上求作一点P,使得点P到AC的距离等于BP的长.(保留作图痕迹,不写作法)
如图,在钝角△ABC中,过钝角顶点B作BD⊥BC交AC于点D.请用尺规作图法在BC边上求作一点P,使得点P到AC的距离等于BP的长.(保留作图痕迹,不写作法)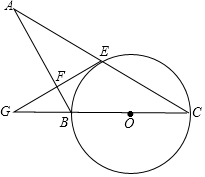 如图,在△ABC中,以BC为直径的⊙O交AC于点E,过点E作EF⊥AB于点F,延长EF交CB的延长线于点G,且∠ABG=2∠C.
如图,在△ABC中,以BC为直径的⊙O交AC于点E,过点E作EF⊥AB于点F,延长EF交CB的延长线于点G,且∠ABG=2∠C.