题目内容
15.矩形的两条对角线的夹角为60°,较短的边长为12cm,则矩形较长的边长12$\sqrt{3}$m.分析 首先证明△AOB是等边三角形,求出AC,在Rt△ABC中,利用勾股定理即可解决问题.
解答 解:如图, ∵四边形ABCD是矩形,
∵四边形ABCD是矩形,
∴OA=OC=OB=OD,∠ABC=90°,
∵∠AOB=60°,
∴△AOB是等边三角形,
∴OA=OB=AB=12cm,AC=2OA=24cm,
在Rt△ABC中,BC=$\sqrt{2{4}^{2}-1{2}^{2}}$=12$\sqrt{3}$(cm).
故答案为:$12\sqrt{3}$.
点评 本题考查矩形的性质、等边三角形的判定和性质、勾股定理等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案
相关题目
 如图,双曲线y=$\frac{2}{x}$(x>0),y=$\frac{12}{x}$(x>0),P、Q为y轴正半轴上两点,设P点的坐标为(0,a-2),PQ=4,分别过P、Q两点作x轴的平行线交两支曲线于C、D、A、B(如图)
如图,双曲线y=$\frac{2}{x}$(x>0),y=$\frac{12}{x}$(x>0),P、Q为y轴正半轴上两点,设P点的坐标为(0,a-2),PQ=4,分别过P、Q两点作x轴的平行线交两支曲线于C、D、A、B(如图)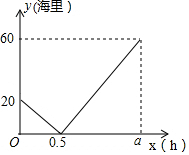 在一条直线上依次有A、B、C三个海岛,某海巡船从A岛出发沿直线匀速经B岛驶向C岛,执行海巡任务,最终达到C岛.设该海巡船行驶x(时)后,与B港的距离为y(海里),y与x之间的函数图象如图所示.
在一条直线上依次有A、B、C三个海岛,某海巡船从A岛出发沿直线匀速经B岛驶向C岛,执行海巡任务,最终达到C岛.设该海巡船行驶x(时)后,与B港的距离为y(海里),y与x之间的函数图象如图所示.
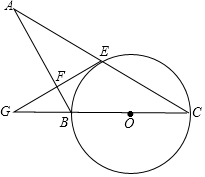 如图,在△ABC中,以BC为直径的⊙O交AC于点E,过点E作EF⊥AB于点F,延长EF交CB的延长线于点G,且∠ABG=2∠C.
如图,在△ABC中,以BC为直径的⊙O交AC于点E,过点E作EF⊥AB于点F,延长EF交CB的延长线于点G,且∠ABG=2∠C.