题目内容
7.某同学做数学题,若每小时做5题,就可以在预定时间完成,当他做完10题后,每题效率提高了60%,因而不但提前3h完成,而且还多做了6题.问:原计划做多少题?多少小时完成?分析 设原计划需要做x小时,提高效率后每小时完成5(1+60%)=8,根据“数学题的总量不变”列出方程并解答.利用时间=总量÷效率来求需要的时间.
解答 解:设原计划需要做x小时,
依题意得:5x=5(1+60%)(x-3-$\frac{10}{5}$)-6,
解得x=12,
原计划做5×12=60(题).
答:原计划做60题,12小时完成.
点评 本题考查了一元一次方程的应用.解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系列出方程,再求解.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
18.某水库养殖场连续用20天时间,采用每天降低水位以减少捕捞成本的办法,对水库中某种鲜鱼进行捕捞、销售.根据调查,整理出第x天(1≤x≤20且x为整数)的捕捞与销售的相关信息如表:
(1)假定该养殖场每天捕捞和销售的鲜鱼没有损失,且能在当天全部售出,求第x天的收入y(元)与x(元)之间的函数关系式;(当天收入=日销售额-日捕捞成本)
(2)试说明(1)中的函数y随x的变化情况,并指出在第几天y取得最大值,最大值是多少?
| 鲜鱼销售单价(元/kg) | 20 |
| 单位捕捞成本(元/kg) | $5-\frac{x}{5}$ |
| 捕捞量(kg) | 950-10x |
(2)试说明(1)中的函数y随x的变化情况,并指出在第几天y取得最大值,最大值是多少?
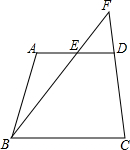 如图,在四边形ABCD中,AD∥BC,点E是边AO的中点,连接BE,BE的延长线交CD的延长线于点F,求证:$\frac{EF}{FB}=\frac{AE}{BC}$.
如图,在四边形ABCD中,AD∥BC,点E是边AO的中点,连接BE,BE的延长线交CD的延长线于点F,求证:$\frac{EF}{FB}=\frac{AE}{BC}$.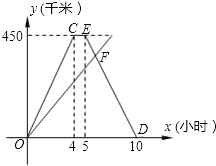 A、B两城间的公路长为450千米,甲、乙两车同时从A城出发沿这一公路驶向B城,甲车到达B城1小时后沿原路返回.如图是它们离A城的路程y(千米)与行驶时间 x(小时)之间的函数图象.
A、B两城间的公路长为450千米,甲、乙两车同时从A城出发沿这一公路驶向B城,甲车到达B城1小时后沿原路返回.如图是它们离A城的路程y(千米)与行驶时间 x(小时)之间的函数图象. 如图所示,AD=BC,试判断AB与CD的大小关系,并说明理由.
如图所示,AD=BC,试判断AB与CD的大小关系,并说明理由.