题目内容
2.?ABCD中,∠BAD的平分线依次与BD、CD交于E,F,与BC的延长线交于C,得出五个结论:(1)AB=BC.
(2)AD=DF.
(3)AE=EF.
(4)BE=ED.
(5)CF=CG,
判断其中有几个结论正确.并说明理由.
分析 根据四边形ABCD是平行四边形,得到AD∥BC,AB∥CD,根据平行线的性质得到∠1=∠G,∠2=∠3,∠2=∠4,∠1=∠G,根据角平分线的定义得到∠1=∠2,等量代换得到∠1=∠3,∠4=∠G,由等腰三角形的判定即可得到结论.
解答 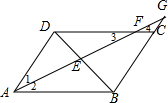 解:有(2)AD=DF,(5)CF=CG两个结论正确;
解:有(2)AD=DF,(5)CF=CG两个结论正确;
理由:∵四边形ABCD是平行四边形,
∴AD∥BC,AB∥CD,
∴∠1=∠G,∠2=∠3,∠2=∠4,∠1=∠G,
∵AF平分∠DAB,
∴∠1=∠2,
∴∠1=∠3,∠4=∠G,
∴AD=DF,CF=CG.
点评 本题考查了平行四边形的性质,等腰三角形的性质,角平分线的定义,平行线的性质,熟练掌握平行四边形的性质是解题的关键.

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案
相关题目
12.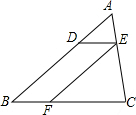 如图,在△ABC中,点D在边AB上,过点D作DE∥BC交AC于点E,过点E作EF∥AB交BC于点F,△EFC的面积记为S1,四边形DEFB的面积为S2.若$\frac{AD}{DB}=\frac{1}{2}$,则S1与S2的大小关系为( )
如图,在△ABC中,点D在边AB上,过点D作DE∥BC交AC于点E,过点E作EF∥AB交BC于点F,△EFC的面积记为S1,四边形DEFB的面积为S2.若$\frac{AD}{DB}=\frac{1}{2}$,则S1与S2的大小关系为( )
 如图,在△ABC中,点D在边AB上,过点D作DE∥BC交AC于点E,过点E作EF∥AB交BC于点F,△EFC的面积记为S1,四边形DEFB的面积为S2.若$\frac{AD}{DB}=\frac{1}{2}$,则S1与S2的大小关系为( )
如图,在△ABC中,点D在边AB上,过点D作DE∥BC交AC于点E,过点E作EF∥AB交BC于点F,△EFC的面积记为S1,四边形DEFB的面积为S2.若$\frac{AD}{DB}=\frac{1}{2}$,则S1与S2的大小关系为( )| A. | S1>S2 | B. | S1<S2 | C. | S1=S2 | D. | 2S1=S2 |
10.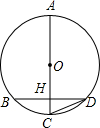 如图,AC为⊙O直径,AC=10,弦BD⊥AC于H,∠BDC=30°,则BH为( )
如图,AC为⊙O直径,AC=10,弦BD⊥AC于H,∠BDC=30°,则BH为( )
 如图,AC为⊙O直径,AC=10,弦BD⊥AC于H,∠BDC=30°,则BH为( )
如图,AC为⊙O直径,AC=10,弦BD⊥AC于H,∠BDC=30°,则BH为( )| A. | $\frac{5}{2}$ | B. | $\frac{{5\sqrt{5}}}{2}$ | C. | $\frac{{5\sqrt{3}}}{2}$ | D. | 4 |
14.若点A(a+1,b-1)在第二象限,则点B(-a,b+2)在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |