题目内容
19.在式子$\frac{1}{a}$,$\frac{20y}{π}$,$\frac{5}{6+x}$,$\frac{x}{7}+\frac{y}{8}$,9x+$\frac{10}{y}$,$\frac{3a{b}^{3}c}{4}$中分式的个数是( )| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
分析 分母中含有字母的代数式叫分式.
解答 解:$\frac{1}{a}$是分式;π是数字不是字母,故$\frac{20y}{π}$不是分式;$\frac{5}{6+x}$是分式;$\frac{x}{7}+\frac{y}{8}$不是分式;9x+$\frac{10}{y}$是分式;$\frac{3a{b}^{3}c}{4}$不是分式.
故选:B.
点评 本题主要考查的是分式的定义,掌握分式的定义是解题的关键.

练习册系列答案
 黄冈创优卷系列答案
黄冈创优卷系列答案
相关题目
10.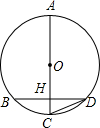 如图,AC为⊙O直径,AC=10,弦BD⊥AC于H,∠BDC=30°,则BH为( )
如图,AC为⊙O直径,AC=10,弦BD⊥AC于H,∠BDC=30°,则BH为( )
 如图,AC为⊙O直径,AC=10,弦BD⊥AC于H,∠BDC=30°,则BH为( )
如图,AC为⊙O直径,AC=10,弦BD⊥AC于H,∠BDC=30°,则BH为( )| A. | $\frac{5}{2}$ | B. | $\frac{{5\sqrt{5}}}{2}$ | C. | $\frac{{5\sqrt{3}}}{2}$ | D. | 4 |
14.若点A(a+1,b-1)在第二象限,则点B(-a,b+2)在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
 已知平面内两点A(0,3),B(-2,-3),分别作出点A关于x轴对称的点A′,点B关于y轴对称的点B′.若点C在y轴,且S△A′B′C=12.试求点C的坐标.
已知平面内两点A(0,3),B(-2,-3),分别作出点A关于x轴对称的点A′,点B关于y轴对称的点B′.若点C在y轴,且S△A′B′C=12.试求点C的坐标.