题目内容
17.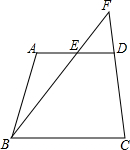 如图,在四边形ABCD中,AD∥BC,点E是边AO的中点,连接BE,BE的延长线交CD的延长线于点F,求证:$\frac{EF}{FB}=\frac{AE}{BC}$.
如图,在四边形ABCD中,AD∥BC,点E是边AO的中点,连接BE,BE的延长线交CD的延长线于点F,求证:$\frac{EF}{FB}=\frac{AE}{BC}$.
分析 根据AD∥BC,推出△FED∽△FBC,由相似三角形的性质得到$\frac{EF}{BF}=\frac{DE}{BC}$,等量代换即可得到结论.
解答 解:∵AD∥BC,
∴△FED∽△FBC,
∴$\frac{EF}{BF}=\frac{DE}{BC}$,
∵点E是边AO的中点,
∴AE=DE,
∴$\frac{EF}{FB}=\frac{AE}{BC}$.
点评 本题考查了相似三角形的判定和性质,线段中点的定义,熟练掌握相似三角形的判定和性质是解题的关键.

练习册系列答案
 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案
相关题目
12.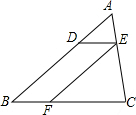 如图,在△ABC中,点D在边AB上,过点D作DE∥BC交AC于点E,过点E作EF∥AB交BC于点F,△EFC的面积记为S1,四边形DEFB的面积为S2.若$\frac{AD}{DB}=\frac{1}{2}$,则S1与S2的大小关系为( )
如图,在△ABC中,点D在边AB上,过点D作DE∥BC交AC于点E,过点E作EF∥AB交BC于点F,△EFC的面积记为S1,四边形DEFB的面积为S2.若$\frac{AD}{DB}=\frac{1}{2}$,则S1与S2的大小关系为( )
 如图,在△ABC中,点D在边AB上,过点D作DE∥BC交AC于点E,过点E作EF∥AB交BC于点F,△EFC的面积记为S1,四边形DEFB的面积为S2.若$\frac{AD}{DB}=\frac{1}{2}$,则S1与S2的大小关系为( )
如图,在△ABC中,点D在边AB上,过点D作DE∥BC交AC于点E,过点E作EF∥AB交BC于点F,△EFC的面积记为S1,四边形DEFB的面积为S2.若$\frac{AD}{DB}=\frac{1}{2}$,则S1与S2的大小关系为( )| A. | S1>S2 | B. | S1<S2 | C. | S1=S2 | D. | 2S1=S2 |
2. 有一种足球是由32块黑白相间的牛皮缝制而成的(如图),黑皮可看作正五边形,白皮可看作正六边形.设白皮有x块,则黑皮有(32-x)块,要求出黑皮、白皮的块数,列出的方程是( )
有一种足球是由32块黑白相间的牛皮缝制而成的(如图),黑皮可看作正五边形,白皮可看作正六边形.设白皮有x块,则黑皮有(32-x)块,要求出黑皮、白皮的块数,列出的方程是( )
 有一种足球是由32块黑白相间的牛皮缝制而成的(如图),黑皮可看作正五边形,白皮可看作正六边形.设白皮有x块,则黑皮有(32-x)块,要求出黑皮、白皮的块数,列出的方程是( )
有一种足球是由32块黑白相间的牛皮缝制而成的(如图),黑皮可看作正五边形,白皮可看作正六边形.设白皮有x块,则黑皮有(32-x)块,要求出黑皮、白皮的块数,列出的方程是( )| A. | 3x=32-x | B. | 3x=5(32-x) | C. | 5x=3(32-x ) | D. | 6x=32-x |
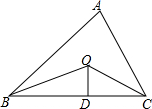 如图,已知△ABC的周长是22,OB、OC分别平分∠ABC和∠ACB,OD⊥BC于D,且OD=3,△ABC的面积是多少?
如图,已知△ABC的周长是22,OB、OC分别平分∠ABC和∠ACB,OD⊥BC于D,且OD=3,△ABC的面积是多少?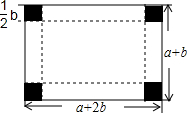 红枣丰收了,为了运输方便,小华的爸爸打算把一个长为(a+2b)cm、宽为(a+b)cm的长方形纸板制成一个有底无盖的盒子,在长方形纸板的四个角各截去一个边长为$\frac{1}{2}$bcm的小正方形,然后沿折线折起即可,如图所示,现将盒子的外表面贴上彩色花板.
红枣丰收了,为了运输方便,小华的爸爸打算把一个长为(a+2b)cm、宽为(a+b)cm的长方形纸板制成一个有底无盖的盒子,在长方形纸板的四个角各截去一个边长为$\frac{1}{2}$bcm的小正方形,然后沿折线折起即可,如图所示,现将盒子的外表面贴上彩色花板.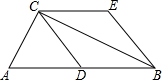 如图,在Rt△ABC中,∠ACB=90°,CD是AB边上的中线,过点B作BE∥CD,过点C作CE∥AB,BE,CE相交于点E.
如图,在Rt△ABC中,∠ACB=90°,CD是AB边上的中线,过点B作BE∥CD,过点C作CE∥AB,BE,CE相交于点E.