题目内容
20．
如图，在Rt△OAB中，OA=2，AB=1，OA在数轴上，点O与原点重合，以原点为圆心，线段OB长为半径画弧，交数轴正半轴于一点，则这个点表示的实数是（ ）| A． | $\sqrt{2}$ | B． | $\sqrt{5}$ | C． | 3 | D． | 2$\sqrt{5}$ |
分析 根据勾股定理求出OB的长，再根据旋转的性质求出这个点表示的数．
解答 解：在Rt△OAB中，OA=2，AB=1，
由勾股定理，OB=$\sqrt{O{A}^{2}+A{B}^{2}}$=$\sqrt{5}$，
则这个点表示的实数是$\sqrt{5}$，
故选：B．
点评 本题考查旋转的性质和实数与数轴的关系以及勾股定理的应用，求出OB的长、理解旋转变化前后，对应线段、对应角分别相等，图形的大小、形状都不改变是解题的关键．
练习册系列答案
阅读快车系列答案
相关题目
5．
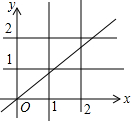如图，若正比例函数y=kx图象与四条直线x=1，x=2，y=1，y=2相交围成的正方形有公共点，则k的取值范围是（ ）
如图，若正比例函数y=kx图象与四条直线x=1，x=2，y=1，y=2相交围成的正方形有公共点，则k的取值范围是（ ）| A． | k≤2 | B． | k≥$\frac{1}{2}$ | C． | 0＜k＜$\frac{1}{2}$ | D． | $\frac{1}{2}$≤k≤2 |
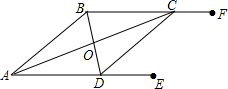如图，AE∥BF，AC平分∠BAD，且交BF于点C，BD平分∠ABC，且交AE于点D，连接CD，求证：
如图，已知AM∥BN，∠A=60°，点P是射线AM上一动点（与A不重合），BC、BD分别平分∠ABP和∠PBN，交射线AM于C、D，（推理时不需要写出每一步的理由）