题目内容
1.已知:x+y=3,xy=-8,求:(1)x2+y2
(2)(x2-1)(y2-1).
分析 (1)原式利用完全平方公式变形,将已知等式代入计算即可求出值;
(2)原式利用多项式乘以多项式法则计算,整理后将各自的值代入计算即可求出值.
解答 解:(1)∵x+y=3,xy=-8,
∴原式=(x+y)2-2xy=9+16=25;
(2)∵x+y=3,xy=-8,
∴原式=x2y2-(x2+y2)+1=64-25+1=40.
点评 此题考查了完全平方公式,熟练掌握完全平方公式是解本题的关键.

练习册系列答案
相关题目
16.如果a<b,下列各式中不一定正确的是( )
| A. | a-1<b-1 | B. | $\frac{1}{a}$<$\frac{1}{b}$ | C. | -3a>-3b | D. | $\frac{a}{4}$<$\frac{b}{4}$ |
6.下列命题是假命题的是( )
| A. | 平分弦的直径垂直于弦 | |
| B. | 不在同一直线上的三点确定一个圆 | |
| C. | 矩形的四个顶点在同一个圆上 | |
| D. | 三角形的内心到三角形三边的距离相等 |
13.下列式子中,属于最简二次根式的是( )
| A. | $\sqrt{16}$ | B. | $\sqrt{6}$ | C. | $\sqrt{28}$ | D. | $\sqrt{\frac{1}{5}}$ |
11.在Rt△ABC中,已知两边长分别是3和4,则第三边长为( )
| A. | 5 | B. | $\sqrt{7}$ | C. | 5或$\sqrt{7}$ | D. | 无法确定 |
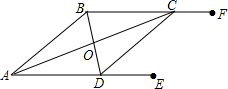 如图,AE∥BF,AC平分∠BAD,且交BF于点C,BD平分∠ABC,且交AE于点D,连接CD,求证:
如图,AE∥BF,AC平分∠BAD,且交BF于点C,BD平分∠ABC,且交AE于点D,连接CD,求证: 如图,已知AM∥BN,∠A=60°,点P是射线AM上一动点(与A不重合),BC、BD分别平分∠ABP和∠PBN,交射线AM于C、D,(推理时不需要写出每一步的理由)
如图,已知AM∥BN,∠A=60°,点P是射线AM上一动点(与A不重合),BC、BD分别平分∠ABP和∠PBN,交射线AM于C、D,(推理时不需要写出每一步的理由)